Читайте также:
|
где основание b > 0.
где основание b > 0.
Предположим, что 
для всех x близких к a, за исключением, быть может, самой точки x = a. Тогда, если
То
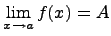
То есть функция f (x) остается "зажатой" между двумя другими функциями, стремящимися к одному и тому же пределу A.
34)Таблица эквивалентных бесконечно малых при 
Поскольку в этой таблице мы всегда будем рассматривать базу , для простоты записи обозначение этой базы будем пропускать и писать знак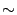 
вместо 
.
1) 
. Эту формулу мы уже доказали и использовали в примерах. Эквивалентность 
и 
при означает в точности, что первый замечательный предел равен 1.
2) 
. Эта эквивалентность тоже была доказана выше в одном из примеров.
3) 
. Докажем эту эквивалентность:
4) 
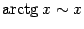. Докажите это в качестве упражнения, сделав замену 
и применив предыдущую табличную формулу.
5) 
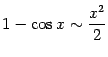. Для доказательства воспользуемся формулой 
. Далее, имеем:
Дата добавления: 2015-08-27; просмотров: 72 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Предел разности равен разности пределов, если каждый из них существует, т.е. | | | И мы доказали формулу 6. |