|
Читайте также: |
О п р е д е л е н и е 1. Точкой разрыва первого рода функции y = f (x) называется такая точка x 0, в которой функция имеет левый и правый пределы, неравные между собой (рис. 69) .
Рис. 69
|  (4.32)
|
О п р е д е л е н и е 2. Точка x 0 (рис. 70) называется точкой разрыва второго рода функции y = f (x), если хотя бы один из односторонних пределов не существует или равен бесконечности:
и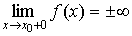 
. (4.33)
Рис. 70
| 
Рис. 71
|  Рис. 72
|
О п р е д е л е н и е 3. Точка x 0 (рис. 71) называется точкой устранимого разрыва y = f (x), если функция в точке неопределена, но односторонние пределы существуют и равны между собой:
, но 
. (4.34)
Такой разрыв можно устранить, доопределив функцию в точке разрыва x 0 значением ее предела А:
Дата добавления: 2015-08-27; просмотров: 70 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Теорема 3. Частное двух непрерывных функций есть функция непрерывная, если знаменатель в рассматриваемой точке не обращается в нуль. | | | ПРОИЗВОДНАЯ ФУНКЦИИ |