Теорема 3. Частное двух непрерывных функций есть функция непрерывная, если знаменатель в рассматриваемой точке не обращается в нуль.

Если функцию можно представить в виде y = f(u), где u = φ(x), т.е. если функция 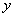зависит от переменной 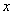через промежуточный аргумент u, то 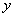называется сложной функцией переменной x.

Примеры:

1. y = sin x³. Здесь u = x³, y = sin u.
2. y = e^{tg x}, u = tg x, y = e^u.

Таким образом, под термином сложная функция следует понимать не какое – либо очень сложное выражение, а функцию, которая зависит от аргумента x через несколько промежуточных функций.

Дата добавления: 2015-08-27