Второй замечательный предел

Второй замечательный предел служит для раскрытия неопределенности 1^∞ и выглядит следующим образом

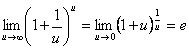
Обратим внимание на то, что в формуле для второго замечательного предела в показателе степени должно стоять выражение, обратное тому, которое прибавляется к единице в основании (так как в этом случае можно ввести замену переменных и свести искомый предел ко второму замечательному пределу).

37)НЕПРЕРЫВНЫЕ ФУНКЦИИ
НЕПРЕРЫВНОСТЬ ФУНКЦИИ В ТОЧКЕ

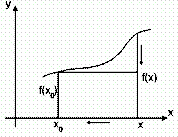Представление о непрерывности функции интуитивно связано у нас с тем, что её графиком является плавная, нигде не прерывающаяся линия. При рассмотрении графика такой функции y = f(x) мы видим, что близким значениям аргумента соответствуют близкие значения функции: если независимая переменная 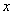приближается к точке x₀, то значение функции y = f(x) неограниченно приближается к значению функции в точке x₀, т.е. к f(x₀).

Дадим строгое определение непрерывности функции. Итак, пусть имеем функцию y = f(x).

Функция y = f(x) называется непрерывной в точке x₀, если она определена в этой точке и в некоторой окрестности содержащей x₀ и

.

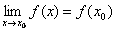(1)

Таким образом, можно сказать, что функция непрерывна в точке x₀, если выполнены 3 условия:

1. она определена в точке x₀ и в некоторой её окрестности;
2. имеет предел при x → x₀;
3. этот предел равен значению функции в точке x₀.

Формулу (1) можно записать в виде 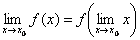, т.к. 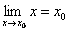. Это означает, что для того, чтобы найти предел непрерывной функции при x → x₀, достаточно в выражение функции подставить вместо аргумента x его значение x₀.

Пример: Докажем, что функция y = 3 x ² непрерывна в произвольной точке x₀. Для этого найдем .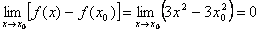

Если функция y=f(x) непрерывна в каждой точке некоторого интервала (a; b), где a < b, то говорят, что функция непрерывна на этом интервале.

Дата добавления: 2015-08-27