
|
Читайте также: |
Приращение, которое получает функция Z=f(x, y), когда изменяется только одна из переменных, называется частным приращением функции по соответствующей переменной: ΔxZ=f(x+Δx,y)-f(x,y), ΔyZ=f(x,y+Δy)-f(x,y).
ОПРЕДЕЛЕНИЕ: Частным дифференциалом по х функции Z=f(x, y) называется главная часть частного приращения ΔxZ=f(x+Δx,y)-f(x,y), пропорциональная приращению Δx независимой переменной х. Аналогично определяется частный дифференциал по у, т.е. ΔyZ=f(y+Δy,x)-f(x,y).
Дифференциалы независимых переменных х и у просто равны их приращениям, т.е. dx=Δx, dy=Δy. Частные дифференциалы обозначаются так: dxZ -частный дифференциал по х, dyZ - частный дифференциал по у. При этом:
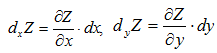
Дата добавления: 2015-08-27; просмотров: 45 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Дифференцируемость функции нескольких переменных. | | | Теорема. Полный дифференциал функции двух независимых переменных равен сумме произведений частных производных функции на дифференциалы соответствующих независимых переменных. |