
Читайте также:
|
Геометрический смысл дифференциала очень просто устанавливается если вспомнить геометрический смысл производной: производная функции в точке равна угловому коэффициенту касательной в данной точке х0. Поэтому, если мы начнем записывать уравнение касательной прямой, проходящей через заданную точку кривой, то мы обнаружим интересную особенность в этом уравнении. Действительно, уравнение, проходящее через точку (x0, y0), с угловым коэффициентом k=f'(x0) имеет вид





следовательно уравнение касательной записывается в виде
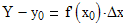
В правой части этого уравнения мы имеем дифференциал функции у в точке х0, а в левой - приращение (или изменение) ординаты касательной. Вот вам и геометрический смысл дифференциала: дифференциал функции в точке равен приращению ординаты касательной к кривой в этой точке.
Таким образом для уяснения геометрического смысла дифференциала функции вовсе не обязательно рисовать графики функции и касательной, а достаточно всего лишь владеть понятием дифференциала, уметь выводить уравнение прямой с угловым коэффициентом, знать геометрический смысл производной и уметь отличать приращение ординаты касательной прямой от приращения значения функции.
Мы написали заглавную букву игрек в уравнении касательной не случайно:

поскольку эта заглавная буква игрек как раз и обозначает значение касательной, а не значение самой функции
46)
Дата добавления: 2015-08-27; просмотров: 49 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Геометрический смысл производной | | | Дифференцируемость функции нескольких переменных. |