Геометрический смысл производной

Рисунок 3.1.2.1. Определение касательной

Возьмем кривую CAB, выберем на ней точку M и проведем секущую AM. Будем приближать по дуге точку M к точке A. В этом случае прямая AM будет поворачиваться вокруг точки A, приближаясь (для гладких линий) к некоторому пределу – прямой AT. Другими словами 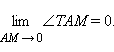Прямую AT, обладающую таким свойством, называют касательной к кривой CAB в точке A.

Угловой коэффициент секущей AM при AM → 0 стремится к угловому коэффициенту касательной AT: Данное равенство справедливо, если в точке A существует невертикальная касательная к кривой CAB.

Если кривая CAB является графиком функции f (x), то для углового коэффициента k касательной можно записать:

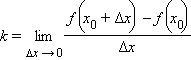
(здесь и далее x ₀ и f (x ₀) – координаты точки касания). Функция f (x) дифференцируема в точке x ₀ тогда и только тогда, когда к графику функции в этой точке можно построить невертикальную касательную, причем угловой коэффициент этой касательной равен производной функции в этой точке:

Другими словами, производная функции в точке x ₀ равняется тангенсу угла наклона касательной к графику функции в этой точке. Уравнение прямой, проходящей через точку (a; b), задается формулой y = k (x – a) + b. Поэтому уравнение касательной вобщем случае выглядит так:

Проходящие через точку A прямые с угловыми коэффициентами и называются, соответственно, левой и правой касательными к графику функции y = f (x) в точке A. Эти касательные совпадают, если функция f дифференцируема в точке A.

Пусть графики функций y = f ₁(x) и y = f ₂(x) пересекаются в точке A. Углом φ между их графиками называется угол, образованный касательными к ним в точке A. В этом случае

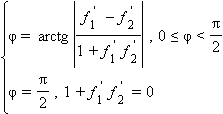
Модель 3.2. Касательная и нормаль

Нормалью к графику функции y = f (x) в точке A (x ₀; y ₀) называется прямая, проходящая через точку A и перпендикулярная касательной к этой точке. Она задается уравнением

что следует из свойства угловых коэффициентов перпендикулярных друг другу прямых.

В случае бесконечной производной касательная в точке x ₀ становится вертикальной и задается уравнением x = x ₀, а нормаль – горизонтальной: y = y ₀.

42) Таблица основных формул дифференцирования

Функция	Производная	Функция	Производная

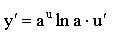
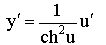
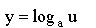
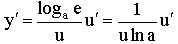
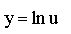
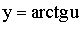
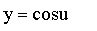
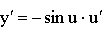
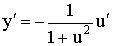
43)Дифференцируемость функции. Пусть . Составим полное приращение функции в точке :

.

Определение. Функция называется дифференцируемой в точке 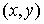, если ее полное приращение в этой точке можно представить в виде

, (1)

где и 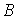– некоторые числа, при , .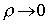

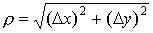Другими словами, функция дифференцируема в точке 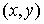, если ее приращение эквивалентно функции : при 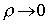. Выражение в этом случае представляет собой главную часть приращения , линейно зависящую от и .

Определение. Если функция дифференцируема в точке 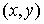, то главную линейную часть ее приращения называют полным дифференциалом в точке 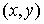и обозначают в виде

.

Для независимых переменных и полагают и . Поэтому полный дифференциал записывают также в виде

.

Формула (1) показывает, что, как и в случае функции одной переменной, верна

Теорема 5. Если функция 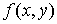дифференцируема в точке 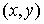, то она непрерывна в этой точке.

Обратное утверждение неверно, т.е. непрерывность является только необходимым, но не достаточным условием дифференцируемости функции. Покажем это.

Пример. Найдем частные производные функции :

.

Полученные формулы теряют смысл в точке .

Можно показать иначе, что функция не имеет частных производных в точке . В самом деле, . Эта функция одной переменной , как известно, не имеет производной в точке . Последнее и означает, что частная производная в точке не существует. Аналогично, не существует частная производная . При этом функция , очевидно, непрерывна в точке . ^

Итак, мы показали, что непрерывная функция может не иметь частных производных. Осталось установить связь между дифференцируемостью и существованием частных производных.

44)Связь между дифференцируемостью и существованием частных производных. Напомним, что для функции одной переменной существование производной в точке является необходимым и достаточным условием дифференцируемости функции в этой точке. Для функции многих переменных дифференцируемость и существование частных производных не являются эквивалентными свойствами функции.

Теорема 6 (необходимое условие дифференцируемости). Если функция дифференцируема в точке , то она имеет в точке частные производные по каждой переменной и .

При этом , , где и 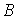– числа из равенства (1). Поэтому условие дифференцируемости (1) можно записать в виде

,

а полный дифференциал функции – в виде

.

Обратная теорема не верна, т.е. существование частных производных не является достаточным условием дифференцируемости функции.

Теорема 7 (достаточное условие дифференцируемости). Если функция имеет непрерывные частные производные и в точке , то она дифференцируема в точке (и ее полный дифференциал в этой точке выражается формулой ).

Обратная теорема не верна, т.е. непрерывность частных производных является только достаточным, но не необходимым условием дифференцируемости функции.

45) Понятие дифференциала функции

Еще раз запишем определение производной (см. Производная функции.Примеры решения.)

Теперь произведем преобразования над этим пределом и воспользуемся понятием бесконечно малой функции. Перенесем значение производной из левой части в правую:

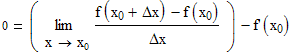
Величина производной функции в данной точке х0 является величиной постоянной, а предел постоянной равен самой этой постоянной:

Разность пределов равна пределу разности, следовательно

или еще преобразуем:

Величина приращения функции записывается более кратко

Равенство этого предела нулю означает, что числитель равен бесконечно малой более высокого порядка относительно знаменателя, то есть относительно приращения независимой переменной. По другому это записывается следующим образом

Таким образом, приращение функции, или зависимой переменой, представляется в виде суммы двух бесконечно малых величин:

· одна - линейная главная часть,

· вторая - бесконечно малая более высокого порядка относительно независимой переменной:

Так вот, эта линейная главная часть

и называется дифференциалом функции f(x) в точке х0 и обозначается

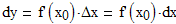
Таким образом, дифференциал равен произведению производной на дифференциал независимой переменной или на приращение независимой переменной, что одно и то же.

Дата добавления: 2015-08-27