Модуль частного равен частному модулей делимого и делителя, а аргумент частного равен разности аргументов делимого и делителя.
ПРОИЗВОДНАЯ ФУНКЦИИ | Геометрический смысл производной | Геометрический смысл дифференциала функции | Дифференцируемость функции нескольких переменных. | Частные и полные дифференциалы. | Теорема. Полный дифференциал функции двух независимых переменных равен сумме произведений частных производных функции на дифференциалы соответствующих независимых переменных. | Определение 1. Если существует предел | Следующее наблюдение, отдавая дань уважения его автору - Евклиду, назовем теоремой. | Теорема. Всякое целое число, отличное от - 1, 0 и 1, единственным образом (с точностью до порядка сомножителей) разложимо в произведение простых чисел. | Комплексные числа |
Если делимое и делитель даны в алгебраической форме, то правило деления таково: для того, чтобы разделить комплексное число (a 1 + b 1 i) на другое комплексное число (a 2 + b 2 i), то есть найти 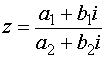 , нужно и числитель, и знаменатель умножить на число, сопряжённое знаменателю.
, нужно и числитель, и знаменатель умножить на число, сопряжённое знаменателю.
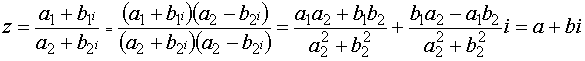 .
.
В результате операции получили элемент того же множества. Значит, операция деления считается введённой.
Возведение в степень комплексных чисел
Дата добавления: 2015-08-27; просмотров: 63 | Нарушение авторских прав
mybiblioteka.su - 2015-2025 год. (0.006 сек.)

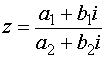 , нужно и числитель, и знаменатель умножить на число, сопряжённое знаменателю.
, нужно и числитель, и знаменатель умножить на число, сопряжённое знаменателю.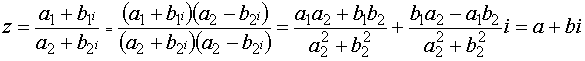 .
.