Комплексные числа

числа вида х + iy, где х и у — действительные числа, а i — так называемая мнимая единица (число, квадрат которого равен —1); х называют действительной частью, а у — мнимой частью К. ч. z = х +iy (обозначают х =Re z, у =Im z). Действительные числа (См.Действительное число) — частный случай К. ч. (при у = 0); К. ч., не являющиеся действительными (у ≠ 0), называют мнимыми числами; при х = 0 К. ч. Называют чисто мнимым. К. ч. z = х+iy и z = х — iy называют комплексно-сопряжёнными. Арифметические действия над К. ч. производятся по обычным правилам действий над многочленами с учётом условия i² = — 1. Геометрически каждое К. ч. х + iy изображается точкой плоскости, имеющей прямоугольные координаты х и у (см. рис.). Если полярные координаты этой точки обозначить через r и φ :, то соответствующее К. ч. можно представить в виде:

r (cosφ + i sin φ)

(тригонометрическая, или полярная, форма К. ч.);

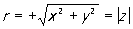
называют модулем К. ч. х+iy, а φ = arg z — аргументом его. Тригонометрическая форма К. ч. особенно удобна для действий возведения в степень и извлечения корня:

[r (cosφ + i sin φ)] ⁿ = rⁿ (cos nφ + i sin n φ) ,

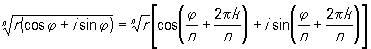
, в частности

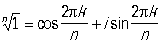
, k = 0, 1, …, n—1

По своим алгебраическим свойствам совокупность К. ч. образует Поле. Это поле алгебраически замкнуто, т. е. любое уравнение xⁿ + a₁x^n-1+...+a_n =0; где a₁,..., a_n — К. ч., имеет (при учёте кратности) среди К. ч. точно n корней.

53) Тригонометрическая форма записи комплексных чисел

Та запись комплексного числа, которую мы использовали до сих пор, называется алгебраической формой записи комплексного числа. Часто бывает удобна немного другая форма записи комплексного числа. Пусть 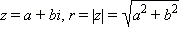и φ = arg z. Тогда по определению аргумента имеем:
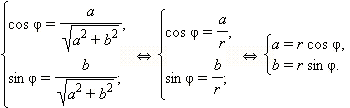Отсюда получается
z = a + bi = r (cos φ + i sin φ). Такая форма называется тригонометрической формой записи комплексного числа. Как видно, для того, чтобы перейти от алгебраической формы записи комплексного числа к тригонометрической форме, нужно найти его модуль и один из аргументов.

Дата добавления: 2015-08-27