|
Читайте также: |
Определение. Произведением двух комплексных чисел называется такое комплексное число, модуль которого равен произведению модулей сомножителей, а аргумент – сумме аргументов сомножителей.
Это определение совершенно очевидно, если использовать показательную форму комплексного числа:
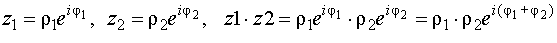
Пусть комплексные числа даны в алгебраической форме. Найдём их произведение: (a 1 + b 1 i) (a 2 + b 2 i) = x + iy.
Имеем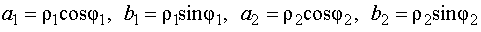 
.
Согласно определению умножения можем записать:
.
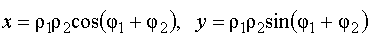Распишем: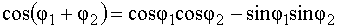 
,
,
.
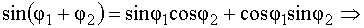
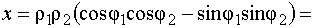
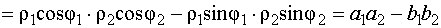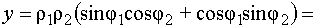
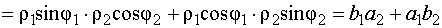Окончательно получим:
.
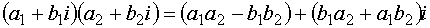Отсюда следует правило умножения комплексных чисел в алгебраической форме: комплексные числа можно перемножать как многочлены.
Если z = а + b i – комплексное число, то число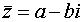 
называется сопряжённым с числом z. Его обозначают при помощи черты над числом.
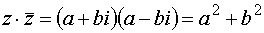, но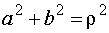 
, следовательно, 
.
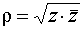Дата добавления: 2015-08-27; просмотров: 34 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Комплексные числа | | | Модуль частного равен частному модулей делимого и делителя, а аргумент частного равен разности аргументов делимого и делителя. |