
Читайте также:
|
Основанием для этого метода служит следующая ТЕОРЕМА:
Пусть данная система АХ=В удовлетворяет условию применимости метода квадратного корня. Тогда существует такая верхнетреугольная матрица S, что: StS=A (8.1)
В этом случае исходную систему можно записать в виде (StS)X=B или St(SX)=B. Если обозначить SX=Y, то весь процесс нахождения решения Х можно разбить на три этапа:
1. Найти матрицу S: StS=A;
2. Найти Y: StY=B;
3. Найти X: SX=Y.
Наиболее трудоемким здесь является первый этап, поскольку на втором и третьем этапе надо лишь решать системы линейных уравнений с нижнетреугольной и верхнетреугольной матрицами соответственно.
Нахождение матрицы S («квадратного корня» из А)
Покажем процесс нахождения коэффициентов матрицы S в случае матрицы А размерами 4х4, а потом уже выпишем общие формулы.
Обозначим элементы матрицы S:
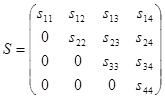
Тогда должно быть выполнено соотношение A=StS, или
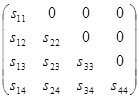
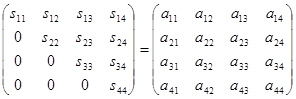
По правилам умножения матриц получаем систему:
s11*s11 = a11
s11*s12 = a12
s11*s13 = a13
s11*s14 = a14
s12*s12 + s22*s22 = a22
s12*s13 + s22*s23 = a23
s12*s14 + s22*s24 = a24
s13*s13 + s23*s23 + s33*s33 = a33
s13*s14 + s23*s24 + s33*s34 = a34
s14*s14 + s24*s24 + s34*s34 + s44*s44 = a44
из 10 уравнений. На первый взгляд, мы сильно усложнили задачу – вместо линейной системы из 4-х уравнений с 4-мя неизвестными мы должны решать систему из 10 нелинейных уравнений с 10 неизвестными. Однако, и в случае 4х4, и в случае N неизвестных наша система решается очень просто: мы по очереди находим все элементы матрицы S. Из 1-го уравнения найдем s11, потом из 2-го уравнения- s12 и т.д. Таким образом мы построчно определим все элементы искомой матрицы.
ОБЩИЕ ФОРМУЛЫ ДЛЯ НАХОЖДЕНИЯ ЭЛЕМЕНТОВ МАТРИЦЫ S имеют вид:
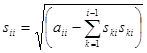 , где i=1,2...n
, где i=1,2...n
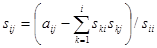 , где j=i+1,...,n
, где j=i+1,...,n
Дата добавления: 2015-08-27; просмотров: 67 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Условие применимости метода квадратного корня. | | | Пример. |