Нахождение наилучшей линейной приближающей функции.

Разберем подробно решение задачи, когда решение ищется в виде линейной функции (вид1). Цель - определить коэффициенты a и b таким образом, чтобы величина

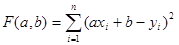
приняла наименьшее значение.

Функция F(a,b) представляет из себя многочлен второй степени относительно величин a и b с неотрицательными значениями, поэтому решение всегда существует. Более того, оно единственно, если узлов больше одного и все они разные.

Задача 5.1. Почему это действительно так? Какую поверхность задает F(a,b)?

Известно, что для поиска экстремумов гладких функций нескольких переменных нужно находить критические точки, т.е. те точки, в которых все частные производные функции равны нулю. В нашем случае необходимо решить следующую систему:

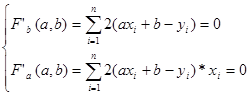
Это система двух линейных уравнений с двумя неизвестными a и b.

Перепишем ее в следующем виде:

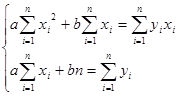
Введем стандартные в статистике обозначения для моментов:

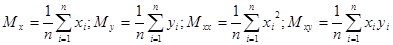
Тогда наша система перепишется в следующем виде:

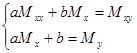
которая решается стандартным образом.

Далее, осталось отметить, что раз критическая точка одна, а мы предварительно определили, что у нашей задачи решение есть, то задача решена полностью.

Разберем ПРИМЕР 5.1 нахождения наилучшей линейной функции.

Пусть зависимость задана таблицей

X	-3	-1
Y

Для ручного вычисления моментов Mx, My, Mxx, Mxy построим таблицу:

	X	Y	X^2	XY
	-3			-9
	-1			-4
Сумма
Среднее значение (М)		6.2		13.4

Отсюда получаем систему

9a+b=13.4 a=0.9

a+b=6.2 или b=5.3

Итак, наилучшая линейная функция имеет вид y=0.9x+5.3

Упражнение 5.1. Проверьте, что если исходные данные удовлетворяют линейной зависимости Yi=а*Xi+b, то и коэффициенты a и b, полученные при решении указанным методом совпадут с исходными.

Упражнение 5.2. Аналогично приведенному выше методу проделайте выкладки и получите систему уравнений для поиска коэффициентов a, b, c при подборе эмпирической квадратичной зависимости (функция вида 2).

Дата добавления: 2015-08-27