
Читайте также:
|
Хорошо известны многочисленные примеры задач из различных отраслей механики, геометрии, физики, и т.д., которые приводят к необходимости вычисления определенных интегралов функции одной переменной на некотором отрезке. Однако, даже в том случае, когда функция задана аналитически, не всегда возможно вычисление точного значения интеграла с помощью формулы Ньютона-Лейбница. Так, нельзя выразить в элементарных функциях первообразные функции sin(x)/x (интегральный синус) или функции e-x*x, которая играет фундаментальную роль в теории вероятностей. Если же функция задана таблично, то решение аналитическими методами вообще невозможно. Во всех этих случаях (а также и тогда, когда интеграл можно вычислить по формуле Ньютона-Лейбница, но вычисления первообразных весьма сложны и громоздки) на помощь приходят численные методы интегрирования, которые позволяют вычислить ответ с нужной точностью простыми методами, почти не зависящими от способа задания функции.
Формулы, по которым происходят эти вычисления называют обычно формулами численного интегрирования или КВАДРАТУРНЫМИ формулами. Они, в общем случае имеют вид:
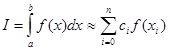 (3.1)
(3.1)
где точки XiÎ[a,b] называются узлами квадратурной формулы, а коэффициенты Сi - весами.
Дата добавления: 2015-08-27; просмотров: 99 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Сплайн-интерполяции. | | | Общая схема |