Читайте также:
|
Для того, чтобы записать интерполяционный многочлен в форме Лагранжа, сначала строят вспомогательные многочлены L0(X), L1(X),..., Ln(X), каждый из которых является многочленом степени n и удовлетворяет условиям:
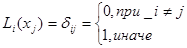, i, j = 0,1,2,..,n.
У каждого из вспомогательных многочленов, тем самым, мы знаем n корней, например, у L2(X) корнями являются X0, X1, X3..., Xn. Kaк известно, многочлен Li(X) по корням можно записать в виде
Li(X)=Ai(X-X0)...(X-Xi-1)(X-Xi+1)...(X-Xn)= Ai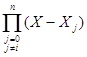 
Чтобы определить величину Ai, остается еще одно условие Li(Xi)=1, откуда:
Дата добавления: 2015-08-27; просмотров: 55 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Постановка задачи интерполирования. | | | Построение многочлена Лагранжа. |