
|
Читайте также: |
Зная вспомогательные многочлены, легко построить и искомый многочлен в виде их линейной комбинации: 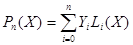
В самом деле, степень Рn(х) не выше n, a подставляя в эту формулу значения Х=Хj, получаем: Рn (Xj)=Уj при j=0,1,2,...,n.
Поскольку ранее мы установили, что многочлен степени n, удовлетворяющий условиям интерполяции в узлах единственен, то построенный многочлен Рn(X) и является искомым. Окончательно, он запишется в виде:
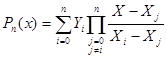
Упражнения: Пользуясь формулой (2.1) выписать интерполяционный многочлен в форме Ньютона для функции, заданной таблицей:
| (2.2) | X | (2.3) | X | -1 | ||||||
| y | y |
Оценка точности формулы (2.1) проводится при предположении, что исходная функция f(x) является (n+1) раз дифференцируемой и мы знаем максимум модуля ее (n+1)-ой производной Mn+1. Как уже отмечалось выше, без дополнительных ограничений на гладкость функции никаких оценок произвести нельзя.
Дата добавления: 2015-08-27; просмотров: 77 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Построение вспомогательных многочленов Лагранжа. | | | Оценка погрешности. |