Вычисление ранга матрицы.

Метод окаймляющих миноров нахождения ранга матрицы.

Определение. Минор М¢ матрицы А называется окаймляющим для минора М, если он получается из последнего добавлением одной новой строки и одного нового столбца матрицы А. Т.о. порядок окаймляющего минора М¢ на единицу больше порядка минора М.

Теорема 7. (доказательство следует из теоремы о базисном миноре). Если для некоторого минора матрицы все окаймляющие миноры равны нулю, то он является базисным.

1) Найти какой-нибудь минор М₁ 1-го порядка (т.е. элемент матрицы), отличный от нуля. Если такого минора нет, то матрица А нулевая и r(A)=0.

2) Вычислять миноры 2-го порядка, содержащие М₁ (окаймляющие миноры) до тех пор, пока не найдется минор М₂, отличный от нуля. Если такого минора нет, то r(A)=1, если есть, то r(A)≥2.

………………

k) Вычислять (если они существуют) миноры k-го порядка, окаймляющие минор M_k-1≠0. Если таких миноров нет, то r(A)=k-1; если есть хотя бы один такой минор, то M_k≠0 r(A)≥k, и процесс продолжается.

Пример. Найдем r(A). А= 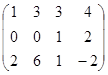. Т.к. есть ненулевые элементы, то r(A)≥1. Найдем ненулевой минор 2-го порядка. Например, М₂= .

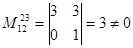Значит, r(A)≥2. Вычислим миноры 3-го порядка, окаймляющие этот минор. 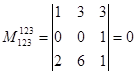, 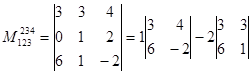=-30+30=0.

Все миноры 3-го порядка, окаймляющие М₂ равны нулю, следовательно, r(A)<3,т.е. r(A)=2. 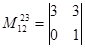- один из базисных миноров.

Метод элементарных преобразований нахождения ранга матрицы:

Матрицу А приводят к ступенчатому виду с помощью элементарных преобразований. Количество ненулевых строк полученной ступенчатой матрицы есть искомый ранг матрицы. Пример. Найти ранг матрицы методом элементарных преобразований.

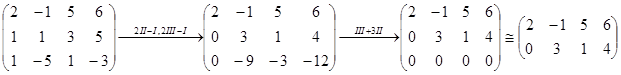
Полученная матрица имеет 2 ненулевые строки, значит ее ранг равен 2. Следовательно, ранг исходной матрицы равен 2. Замечание. Если а₁₁=0, то перестановкой строк или столбцов добиваемся того, чтобы а₁₁≠0.

Дата добавления: 2015-08-27