Система n линейных уравнений с n неизвестными.

Пусть дана квадратная система, т.е. m=n, 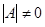, т.е. матрица системы квадратная и невырожденная. Δ=|А| - определитель системы.

Теорема 1. СЛАУ с квадратной невырожденной матрицей имеет и притом единственное решение.

Доказательство. Покажем сначала единственность решения (в предположении, что оно существует). Пусть существуют n чисел х₁,х₂,…,х_n такие, что при подстановке в систему все уравнения системы обращаются в верные тождества:

(8)

Тогда умножая тождества (8) соответственно на алгебраические дополнения A_1j, A_2j,…,A_nj элементов j-го столбца определителя D матрицы А= и складывая полученные при этом тождества, получим "j=1,2,…,n:

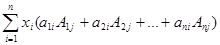=b₁A_1j+b₂A_2j+…+b_nA_nj.

Т.к., по свойствам определителя, , то из последнего равенства получаем, что x_jD=b₁A_1j+b₂A_2j+…+b_nA_nj (9)

Обозначим Δ_j – определитель матрицы, получаемой из матрицы системы А заменой j-го столбца столбцом свободных членов.

Тогда равенство (9) примет вид: x_jD=Δ_j.

В итоге получаем (j=1,2,…,n) (10) – формулы Крамера (Габриэль Крамер (1704-1752) – швейцарский математик).

Т.о., если решение квадратно системы существует, то оно однозначно определяется формулами (10).

Докажем теперь существование решения. Покажем, что rg (A|В)=rg A.

Т.к. D¹0, то rg A=n, а расширенная матрица (A|В) содержит только n строк, следовательно rg (A|В)£nÞ rg (A|В)=n=rg A ч.т.д.

Матричный способ решения СЛАУ (при помощи А^-1).

Матричная запись СЛАУ: АХ=В. (6)

Т.к. матрица системы А квадратная и невырожденная, то существует обратная матрица А^-1.Умножая слева обе части матричного равенства (2) на А^-1, получим А^-1(АХ)=А^-1В. Т.к. А^-1(АХ)= (А^-1А)Х=ЕХ=Х, то решением системы методом обратной матрицы будет матрица-столбец:

Х_nx1=А_nxn^-1В_nx1 (11)

Пример. , , , 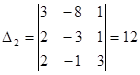. х₁=-4, х₂=1, х₃=2. А^-1=

Дата добавления: 2015-08-27