Алгоритм вычисления обратной матрицы. (Метод присоединенной матрицы).

1) Находим . Если =0, то матрица вырожденная и А^-1 не существует. Если 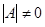, то А невырожденная и А^-1 существует.

2) Находим А^Т.

3) Находим алгебраические дополнения элементов транспонированной матрицы , (i=1,2,…,n; j=1,2,…,n) и составляем из них присоединенную матрицу : 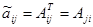(i=1,2,…,n; j=1,2,…,n).

4) Вычисляем обратную матрицу по формуле (10).

5) Проверяем правильность вычисления А^-1 по определению:А^-1А=Е.

Пример. А= 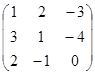, -5, А^Т=

А₁₁=-4 А₁₂=3 А₁₃=-5 А₂₁=-8 А₂₂=6 А₂₃=-5 А₃₁=-5 А₃₂=5 А₃₃=-5

А^-1=

Для невырожденных матриц выполняются следующие свойства:

1. ; 3. 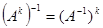; 5. (А^-1)^Т=(А^Т)^-1.

2. (А^-1)^-1=А; 4. (АВ)^-1=В^-1А^-1;

Дата добавления: 2015-08-27