Если элементы двух строк (столбцов) определителя пропорциональны, то определитель равен 0.

Доказательство. По свойству 5 коэффициент пропорциональности λ можно вынести за знак определителя, после чего останется определитель с двумя одинаковыми строками: Δ^΄=λΔ, где Δ имеет две одинаковые строки и по свойству 4 равен 0. ч.т.д.

Определитель не изменится, если к элементам какой-либо строки (столбца) матрицы прибавить элементы другой строки (столбца), предварительно умноженные на одно и то же число.

Доказательство. Полученный в результате указанного прибавления определитель, по свойству 3, можно разбить на сумму двух определителей, один из которых равен исходному, а второй равен 0 в силу пропорциональности двух строк (столбцов) и свойства 7.: D¢=D+0. ч.т.д.

Свойство алгебраических дополнений соседних строк (столбцов).

Сумма произведений элементов какой-либо строки (столбца) определителя на соответствующие алгебраические дополнения элементов другой строки (столбца) этого определителя равна 0, т.е..

Доказательство. Докажем для строк (для столбцов доказательство аналогично). Запишем разложение определителя D по i-й строке:

Δ= 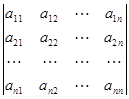=a_i1A_i1+a_i2A_i2+…+a_inA_in (7)

Т.к. алгебраические дополнения A_i1, A_i2,…,A_in не зависят от элементов i-й строки a_i1,a_i2,…,а_in, то равенство (70 является тождеством относительно a_i1,a_i2,…,а_in и сохраняется при замене чисел a_i1,a_i2,…,а_in любыми другими n числами. Заменив a_i1,a_i2,…,а_in соответствующими элементами любой (отличной от i-й) k-й строки a_k1,a_k2,…,а_kn, получим слева в (7) определитель с двумя одинаковыми строками a_k1,a_k2,…,а_kn, равный нулю по свойству 4. Таким образом:

a_k1A_i1+a_k2A_i2+…+a_knA_in=0 "i¹k. Ч.т.д.

Сумма произведений произвольных чисел с1,с2,…,сn на алгебраические дополнения элементов любой строки (столбца) равна определителю матрицы. Полученной из данной заменой элементов этой строки (столбца) на числа с1,с2,…,сn.

Свойство также следует из формулы (7).

Дата добавления: 2015-08-27