Читайте также:
|
Пример.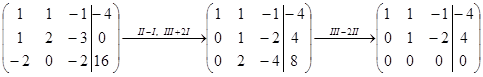 
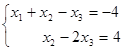
Т.к. r(A)=r(A*)=2<3=n, то система совместна и неопределенна. Кол-во главных переменных равно r(A)=3, кол-во свободных переменных – (n-r)=1. Выберем ненулевой минор 2-го порядка, например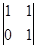 
. Его столбцы – 1-й и 2-й столбцы А- соответсвуют переменным х1 и х2, а х3-свободная переменная. Обозначим х3=с, тогда х2=4+2с, х1=-8-с. Частное решение системы при с=0: (-8;4;0)
Достоинства метода Гаусса: 1 ) значительно менее трудоемкий; 2) позволяет однозначно установить, совместна система или нет, а в случае совместности найти ее решения; 3) дает возможность найти ранг матрицы системы.
Дата добавления: 2015-08-27; просмотров: 54 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Система m уравнений с n неизвестными. | | | Однородные системы линейных уравнений. |