Система m уравнений с n неизвестными.

Рассмотрим решение системы m уравнений с n неизвестными. Допустим она совместна и rg (A|В)=rg A=r.

Пусть r<n. r переменных х₁, х₂,…,х_r называются базисными (зависимыми, основными), если определитель матрицы из коэффициентов при них (т.е. базисный минор) отличен от нуля. Остальные n-r называются свободными (независимыми, неосновными).

Решение системы (1), в котором все n-r свободных переменных равны нулю, называется базисным.

Т.к. каждому разбиению переменных на базисные и свободные соответствует одно базисное решение, а число способов разбиения не превосходит числа сочетаний 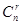, то и базисных решений не более 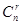. Т.о. совместная система m линейных уравнений с n переменными (m<n) имеет бесконечное множество решений, среди которых базисных решений конечное число, не превосходящее .

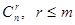Не ограничивая общности, будем считать, что базисный минор матрицы А расположен в верхнем левом углу.

Тогда первые r строк как основной, так и расширенной матрицы являются базисными и, следовательно (по теореме о базисном миноре) каждая из строк расширенной матрицы, начиная с (r+1)-й, является линейной комбинацией первых r строк.

Это означает, что каждое из уравнений системы, начиная с (r+1)-го, является линейной комбинацией (т.е. следствием) первых r уравнений.

Т.о. достаточно найти все решения только первых r уравнений. Запишем первые r уравнений в виде:

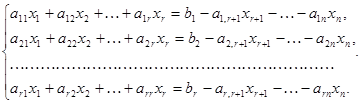(12)

Если задать свободным неизвестным х_r+1,х_r+2,…,x_n произвольные значения, то относительно базисных неизвестных получим квадратную СЛАУ с невырожденной матрицей, у которой существует единственное решение. Т.о., произвольно выбранный набор чисел с_r+1,с_r+2,…,с_n однозначно определяют совокупность r чисел c₁,c₂,…,c_r, обращающих в тождество все уравнения системы (12) и определяющиеся по формулам Крамера.

Обозначим символом M_j(d_i) определитель, получающийся из базисного минора М матрицы системы заменой его j-го столбца столбцом из чисел d₁,d₂,…,d_i,…,d_r (с сохранением без изменения всех остальных столбцов М). Тогда, записывая решение системы (12) с помощью формул Крамера и пользуясь линейным свойством определителя, получим:

c_j= 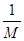M_j(b_i-a_i,r+1c_r+1-…-a_inc_n)= 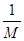(M_j(b_i)-c_r+1M_j(a_i,r+1)-…-c_nM_j(a_in)) j=1,2,…,r (13)

Формулы (13) выражают значения неизвестных x_j=c_j (j=1,2,…,r) через коэффициенты при неизвестных, свободные члены и произвольно заданные параметры c_r+1,…,c_n.

Докажем, что формулы (13) содержат любое решение системы (1). Пусть 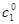, ,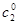…, , 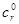,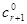…, 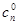- произвольное решение системы (1), тогда оно является и решением системы (12). Но из системы (12) величины 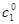, ,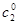…, 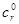однозначно определяются через величины 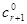,…, 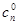по формулам Крамера (13). Т.о. при 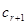= 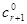,…, 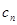= 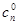формулы (13) дают рассматриваемое решение , ,…, , ,…, .

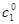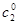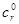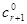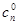Если rg (A|В)=rg A=r=n, то соотношения (13) переходят в формулы:

c_j= 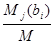j=1,2,…,r определяющие единственное решение системы (1). Т.о. система (1) является определенной, если rg (A|В)=rg A=r=n£m.

Метод Гаусса – метод последовательного исключения переменных – заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого или треугольного вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.

Пусть в системе (1) а₁₁ 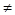0 (этого всегда можно добиться при помощи элементарных преобразований). В 1-м уравнении оставляем переменную х₁, во всех остальных уравнениях исключаем ее, умножая 1-е уравнение на подходящие числа (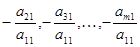) и прибавляя к соответственно 2-му, 3-му,…,m-му уравнению системы.

Далее, предполагая а₂₂ 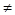0, аналогичным образом исключаем переменную х₂ из всех уравнений, начиная с 3-го. И т.д.

В результате последовательного исключения переменных получаем систему следующего вида:

(14), где r≤m.

Число нуль в последних m-r уравнениях означает, что их левые части имеют вид 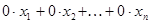. Если хотя бы одно из чисел 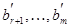не равно нулю, то соответствующее равенство противоречиво, и система (14) несовместна.

Т.о. для любой совместной системы числа 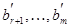в системе (14) не равны нулю. Тогда последние m-r строчки являются тождествами и их можно отбросить при решении системы.

Если r<m (число уравнений меньше числа неизвестных), то система (14) неопределенна и имеет ступенчатый вид.

Если r=m, то система (14) определена и имеет треугольный вид.

Переход системы (1) к равносильной ей системе (14) называется прямым ходом метода Гаусса, а нахождение переменных из системы (14) – обратным ходом.

Преобразования Гаусса удобно проводить не с самими уравнениями, а с расширенной матрицей системы А^*.

Если система определена, то прямой и обратный ход метода Гаусса можно проводить одновременно: (А|В)~(Е|Х). Вместо столбца свободных членов получаем столбец неизвестных.

Пример.

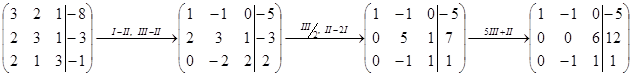
Дата добавления: 2015-08-27