Читайте также:
|
Рассмотрим однородную систему m линейных уравнений с n переменными:
(15)
Система однородных линейных уравнений всегда совместна, т.к. она всегда имеет нулевое (тривиальное) решение (0,0,…,0).
Если в системе (15) m=n и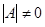 
, то система имеет только нулевое решение, что следует из теоремы и формул Крамера.
Дата добавления: 2015-08-27; просмотров: 60 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Пример с. 75. | | | Теорема 1. Однородная система (15) имеет нетривиальное решение тогда и только тогда, когда ранг ее матрицы меньше числа переменных,т.е. r(A)<n. |