
Читайте также:
|
Доказательство. Существование нетривиального решения системы (15) эквивалентно линейной зависимости столбцов матрицы системы (т.е. существуют такие числа х1, x2,…,xn, не все равные нулю, что справедливы равенства (15)).
По теореме о базисном миноре столбцы матрицы линейно зависимы Û, когда не все столбцы этой матрицы являются базисными, т.е. Û, когда порядок r базисного минора матрицы меньше числа n ее столбцов. Ч.т.д.
Следствие. Квадратная однородная система имеет нетривиальные решения Û, когда |А|=0.
Теорема 2. Если столбцы х(1),х(2),…,х(s) решения однородной системы АХ=0, то любая их линейная комбинация так же является решением этой системы.
Доказательство. Рассмотрим любую комбинацию решений:
х=  , lkÎR
, lkÎR
Тогда АХ=А( )=
)=  =
=  =0. ч.т.д.
=0. ч.т.д.
Следствие 1. Если однородная система имеет нетривиальное решение, то она имеет бесконечно много решений.
Т.о. необходимо найти такие решения х(1),х(2),…,х(s) системы Ах=0, чтобы любое другое решение этой системы представлялось в виде их линейной комбинации и притом единственным образом.
Определение. Система k=n-r (n –количество неизвестных в системе, r=rg A) линейно независимых решений х(1),х(2),…,х(k) системы Ах=0 называется фундаментальной системой решений этой системы.
Теорема 3. Пусть дана однородная система Ах=0 с n неизвестными и r=rg A. Тогда существует набор из k=n-r решений х(1),х(2),…,х(k) этой системы, образующих фундаментальную систему решений.
Доказательство. Не ограничивая общности, можно считать, что базисный минор матрицы А расположен в верхнем левом углу. Тогда, по теореме о базисном миноре, остальные строки матрицы А являются линейными комбинациями базисных строк. Это означает, что если значения х1,х2,…,xn удовлетворяют первым r уравнениям т.е. уравнениям, соответствующим строкам базисного минора), то они удовлетворяют и другим уравнениям. Следовательно, множество решений системы не изменится, если отбросить все уравнения начиная с (r+1)-го. Получим систему:

Перенесем свободные неизвестные хr+1,хr+2,…,xn в правую часть, а базисные х1,х2,…,xr оставим в левой:
 (16)
(16)
Т.к. в этом случае все bi=0, то вместо формул
cj= 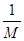 (Mj(bi)-cr+1Mj(ai,r+1)-…-cnMj(ain)) j=1,2,…,r ((13), получим:
(Mj(bi)-cr+1Mj(ai,r+1)-…-cnMj(ain)) j=1,2,…,r ((13), получим:
cj=- 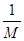 (cr+1Mj(ai,r+1)-…-cnMj(ain)) j=1,2,…,r (13¢)
(cr+1Mj(ai,r+1)-…-cnMj(ain)) j=1,2,…,r (13¢)
Если задать свободным неизвестным хr+1,хr+2,…,xn произвольные значения, то относительно базисных неизвестных получим квадратную СЛАУ с невырожденной матрицей, у которой существует единственное решение. Т.о., любое решение однородной СЛАУ однозначно определяется значениями свободных неизвестных хr+1,хr+2,…,xn. Рассмотрим следующие k=n-r серий значений свободных неизвестных:
 =1,
=1,  =0, ….,
=0, …., 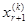 =0,
=0,
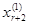 =1,
=1,  =0, ….,
=0, …., 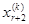 =0, (17)
=0, (17)
………………………………………………
 =1,
=1,  =0, ….,
=0, …., 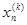 =0,
=0,
(Номер серии указан верхним индексом в скобках, а серии значений выписаны в виде столбцов. В каждой серии  =1, если i=j и
=1, если i=j и  =0, если i¹j.
=0, если i¹j.
i-й серии значений свободных неизвестных однозначно соответствуют значения  ,
,  ,…,
,…,  базисных неизвестных. Значения свободных и базисных неизвестных в совокупности дают решения системы (17).
базисных неизвестных. Значения свободных и базисных неизвестных в совокупности дают решения системы (17).
Покажем, что столбцы еi=  , i=1,2,…,k (18)
, i=1,2,…,k (18)
образуют фундаментальную систему решений.
Т.к. эти столбцы по построению являются решениями однородной системы Ах=0 и их количество равно k, то остается доказать линейную независимость решений (16). Пусть есть линейная комбинация решений e1,e2,…,ek (х(1), х(2),…,х(k)), равная нулевому столбцу:
l 1e1+ l2 e2+…+ lk ek ( l1 х (1)+l2 х (2)+…+lk х (k)= 0)
Тогда левая часть этого равенства является столбцом, компоненты которого с номерами r+1,r+2,…,n равны нулю. Но (r+1)-я компоненты равна l11+l20+…+lk0=l1. Аналогично, (r+2)-я компонента равна l2,…, k-я компонента равна lk. Поэтому l1 = l2 = …=lk=0, что и означает линейную независимость решений e1,e2,…,ek ( х(1), х(2),…,х(k)).Ч.т.д.
Построенная фундаментальная система решений (18) называется нормальной. В силу формулы (13¢) она имеет следующий вид:
 (20)
(20)
Следствие 2. Пусть e1,e2,…,ek -нормальная фундаментальная система решений однородной системы, тогда множество всех решений можно описать формулой:
х=с1 e1 +с2 e2 +…+сk ek (21)
где с1,с2,…,сk – принимают произвольные значения.
Доказательство. По теореме 2 столбец (19) является решением однородной системы Ах=0. Остается доказать, что любое решение  этой системы можно представить в виде (17). Рассмотрим столбец х =уr+1 e1 +…+yn ek. Этот столбец совпадает со столбцом у по элементам с номерами r+1,…,n и является решением (16). Поэтому столбцы х и у совпадают, т.к. решения системы (16) определяются однозначно набором значений ее свободных неизвестных xr+1,…,xn, а у столбцов у и х эти наборы совпадают. Следовательно, у = х = уr+1 e1 +…+yn ek, т.е. решение у является линейной комбинацией столбцов e1,…,yn нормальной ФСР. Ч.т.д.
этой системы можно представить в виде (17). Рассмотрим столбец х =уr+1 e1 +…+yn ek. Этот столбец совпадает со столбцом у по элементам с номерами r+1,…,n и является решением (16). Поэтому столбцы х и у совпадают, т.к. решения системы (16) определяются однозначно набором значений ее свободных неизвестных xr+1,…,xn, а у столбцов у и х эти наборы совпадают. Следовательно, у = х = уr+1 e1 +…+yn ek, т.е. решение у является линейной комбинацией столбцов e1,…,yn нормальной ФСР. Ч.т.д.
Доказанное утверждение справедливо не только для нормальной ФСР, но и для произвольной ФСР однородной СЛАУ.
Х=c1Х1+c2Х2+…+сn-rХn-r - общее решение системы линейных однородных уравнений
Где Х1,Х2,…,Хn-r – любая фундаментальная система решений,
c1,c2,…,сn-r – произвольные числа.
Пример. (с. 78)
Установим связь между решениями неоднородной СЛАУ 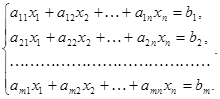 (1) и соответствующей ей однородной СЛАУ
(1) и соответствующей ей однородной СЛАУ  (15)
(15)
Теорема 4. Сумма любого решения неоднородной системы (1) и соответствующей ей однородной системы (15) является решением системы (1).
Доказательство. Если c1,…,cn – решение системы (1), а d1,…,dn - решение системы (15), то подставив в любое (например, в i-е) уравнение системы (1) на место неизвестных числа c1+d1,…,cn+dn, получим:
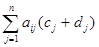 =
=  +
+  =bi+0=bi ч.т.д.
=bi+0=bi ч.т.д.
Теорема 5. Разность двух произвольных решений неоднородной системы (1) является решением однородной системы (15).
Доказательство. Если c¢1,…,c¢n и c²1,…,c²n – решения системы (1), то подставив в любое (например, в i-е) уравнение системы (1) на место неизвестных числа c¢1-с²1,…,c¢n-с²n, получим:
 =
= 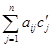 -
-  =bi-bi=0 ч.т.д.
=bi-bi=0 ч.т.д.
Из доказанных теорем следует, что общее решение системы m линейных однородных уравнений с n переменными равно сумме общего решения соответствующей ей системы однородных линейных уравнений (15) и произвольного числа частного решения этой системы (15).
Хнеод.=Хобщ. одн.+Хчаст. неодн. (22)
В качестве частного решения неоднородной системы естественно взять то его решение, которое получается, если в формулах cj= 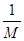 (Mj(bi)-cr+1Mj(ai,r+1)-…-cnMj(ain)) j=1,2,…,r ((13) положить равными нулю все числа cr+1,…,cn,т.е.
(Mj(bi)-cr+1Mj(ai,r+1)-…-cnMj(ain)) j=1,2,…,r ((13) положить равными нулю все числа cr+1,…,cn,т.е.
Х0=( ,…,
,…, 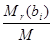 ,0,0,…,0) (23)
,0,0,…,0) (23)
Складывая это частное решение с общим решением Х=c1Х1+c2Х2+…+сn-rХn-r соответствующей однородной системы, получаем:
Хнеод.=Х0+С1Х1+С2Х2+…+Сn-rХn-r (24)
Рассмотрим систему двух уравнений с двумя переменными:
 в которой хотя бы один из коэф. aij
в которой хотя бы один из коэф. aij 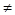 0.
0.
Для решения исключим х2, умножив первое уравнение на а22, а второе – на (-а12) и сложив их:  Исключим х1, умножив первое уравнение на (-а21), а второе – на а11 и сложив их:
Исключим х1, умножив первое уравнение на (-а21), а второе – на а11 и сложив их: 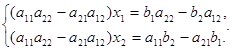 Выражение в скобках – определитель
Выражение в скобках – определитель 
Обозначив  ,
,  , тогда система примет вид:
, тогда система примет вид:  , т.о., если
, т.о., если  , то система имеет единственное решение:
, то система имеет единственное решение:  ,
,  .
.
Если Δ=0, а  (или
(или  ), то система несовместна, т.к. приводится к виду
), то система несовместна, т.к. приводится к виду  Если Δ=Δ1=Δ2=0, то система неопределенная, т.к. приводится к виду
Если Δ=Δ1=Δ2=0, то система неопределенная, т.к. приводится к виду 
Дата добавления: 2015-08-27; просмотров: 129 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Однородные системы линейных уравнений. | | | Классификация |