Линейная зависимость строк.

Понятие ранга матрицы связано с понятием линейной зависимости (независимости) строк (столбцов) матрицы. Рассмотрим это понятие для строк. Для столбцов – аналогично.

Обозначим стоки матрицы А:

е₁=(а₁₁,а₁₂,…,а_1n); е₂=(а₂₁,а₂₂,…,а_2n);…, е_m=(а_m1,а_m2,…,а_mn)

e_k=e_s если a_kj=a_sj, j=1,2,…,n

Арифметические операции над строками матрицы (сложение, умножение на число) вводятся как операции, проводимые поэлементно: λе_k=(λа_k1,λа_k2,…,λа_kn);

e_k+е_s=[(а_k1+a_s1),(a_k2+a_s2),…,(а_kn+a_sn)].

Строка е называется линейной комбинацией строк е₁, е₂,…,е_k, если она равна сумме произведений этих строк на произвольные действительные числа:

е=λ₁е₁+λ₂е₂+…+λ_kе_k

Строки е₁, е₂,…,е_m называются линейно зависимыми, если существуют действительные числа λ₁,λ₂,…,λ_m, не все равные нулю, что линейная комбинация этих строк равна нулевой строке: λ₁е₁+λ₂е₂+…+λ_mе_m= 0,где 0 =(0,0,…,0) (1)

Если линейная комбинация равна нулю тогда и только тогда, когда все коэффициенты λ_i равны нулю (λ₁=λ₂=…=λ_m=0), то строки е₁, е₂,…,е_m называются линейно независимыми.

Теорема 1. Для того, чтобы строки е₁,е₂,…,е_m были линейно зависимы, необходимо и достаточно, чтобы одна из этих строк была линейной комбинацией остальных строк.

Доказательство. Необходимость. Пусть строки е₁, е₂,…,е_m линейно зависимы. Пусть, для определенности в (1) λ_m≠0, тогда

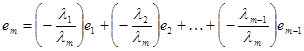
или

Т.о. строка е_m является линейной комбинацией остальных строк. Ч.т.д.

Достаточность. Пусть одна из строк, например е_m, является линейной комбинацией остальных строк. Тогда найдутся числа 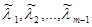такие, что выполняется равенство , которое можно переписать в виде ,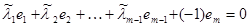

где хотя бы 1 из коэффициентов, (-1), не равен нулю. Т.е. строки линейно зависимы. Ч.т.д.

Определение. Минором k-го порядка матрицы А размера mxn называется определитель k-го порядка с элементами, лежащими на пересечении любых k строк и любых k столбцов матрицы А. (k≤min(m,n)). .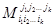

Пример. 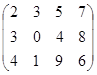, миноры 1-го порядка: = , = ;

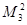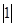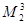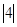миноры 2-го порядка: 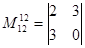, 3-го порядка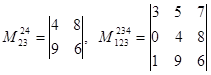

У матрицы 3-го порядка 9 миноров 1-го порядка, 9 миноров 2-го порядка и 1 минор 3-го порядка (определитель этой матрицы).

Определение. Рангом матрицы А называется наивысший порядок отличных от нуля миноров этой матрицы. Обозначение - rg A или r(A).

Свойства ранга матрицы.

1) ранг матрицы A_nxm не превосходит меньшего из ее размеров, т.е.

r(A)≤min(m,n).

2) r(A)=0 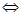когда все элементы матрицы равны 0, т.е. А=0.

3) Для квадратной матрицы А n –го порядка r(A)=n 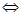, когда А невырожденная.

(Ранг диагональной матрицы равен количеству ее ненулевых диагональных элементов).

4) Если ранг матрицы равен r, то матрица имеет хотя бы один минор порядка r, не равный нулю, а все миноры больших порядков равны нулю.

Для рангов матрицы справедливы следующие соотношения:

1) r(A^T)=r(A)

2) r(A+B)≤r(A)+r(B); 3) r(AB)≤min{r(A),r(B)};

3) r(A+B)≥│r(A)-r(B)│; 4) r(A^TA)=r(A);

5) r(AB)=r(A), если В - квадратная невырожденная матрица.

6) r(AB)≥r(A)+r(B)-n, где n-число столбцов матрицы А или строк матрицы В.

Определение. Ненулевой минор порядка r(A) называется базисным минором. (У матрицы А может быть несколько базисных миноров). Строки и столбцы, на пересечении которых стоит базисный минор, называются соответственно базисными строками и базисными столбцами.

Теорема 2 (о базисном миноре). Базисные строки (столбцы) линейно независимы. Любая строка (любой столбец) матрица А является линейной комбинацией базисных строк (столбцов).

Доказательство. (Для строк). Если бы базисные строки были линейно зависимы, то по теореме (1) одна из этих строк была бы линейной комбинацией других базисных строк, тогда, не изменяя величины базисного минора, можно вычесть из этой строки указанную линейную комбинацию и получить нулевую строку, а это противоречит тому, что базисный минор отличен от нуля. Т.о. базисные строки линейно независимы.

Докажем, что любая строка матрицы А является линейной комбинацией базисных строк. Т.к. при произвольных переменах строк (столбцов) определитель сохраняет свойство равенства нулю, то, не ограничивая общности, можно считать, что базисный минор находится в верхнем левом углу матрицы

А= 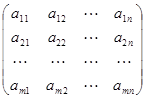, т.е. расположен на первых r строках и первых r столбцах. Пусть 1£j£n, 1£i£m. Покажем, что определитель (r+1)-го порядка

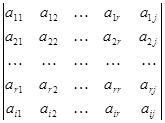равен 0.

Если j£r или i£r, то этот определитель равен нулю, т.к. у него будет два одинаковых столбца или две одинаковых строки.

Если же j>r и i>r, то этот определитель является минором (r+1)-го порядка матрицы А. Т.к. ранг матрицы равен r, значит любой минор большего порядка равен 0.

Раскладывая его по элементам последнего (добавленного) столбца, получаем

a_1jA_1j+a_2jA_2j+…+a_rjA_rj+a_ijA_ij=0, где последнее алгебраическое дополнение A_ij совпадает с базисным минором М_r и поэтому A_ij= М_r≠0.

Разделив последнее равенство на A_ij, можем выразить элемент a_ij, как линейную комбинацию: 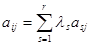, где .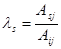

Зафиксируем значение i (i>r) и получаем, что для любого j (j=1,2,…,n) элементы i-й строки e_i линейно выражаются через элементы строк е₁, е₂,…,е_r, т.е. i-я строка является линейной комбинацией базисных строк: . Ч.т.д.

Теорема 3. (необходимое и достаточное условие равенства нулю определителя). Для того, чтобы определитель n-го порядка D был равен нулю, необходимо и достаточно, чтобы его строки (столбцы) были линейно зависимы.

Доказательство (с.40). Необходимость. Если определитель n-го порядка D равен нулю, то базисный минор его матрицы имеет порядок r<n. Тогда хотя бы одна из его строк является не базисной. По теореме 2 эта строка является линейной комбинацией базисных строк. В эту линейную комбинацию можно включить и все оставшиеся строки с коэффициентами 0.

Т.о., одна строка является линейной комбинацией других остальных. Тогда по теореме 1 строки определителя линейно зависимы.

Достаточность. Если строки D линейно зависимы, то по теореме 1 одна строка А_i является линейной комбинацией остальных строк. Вычитая из строки А_i указанную линейную комбинацию, не изменив величины D, получим нулевую строку. Следовательно, по свойствам определителей, D=0. ч.т.д.

Т.о. можно считать, что ранг матрицы равен максимальному числу ее линейно независимых строк или столбцов.

Теорема 4. При элементарных преобразованиях ранг матрицы не меняется.

Доказательство. Как было показано при рассмотрении свойств определителей, при преобразованиях квадратных матриц их определители либо не изменяются, либо умножаются на ненулевое число, либо меняют знак. При этом наивысший порядок отличных от нуля миноров исходной матрицы сохраняется, т.е. ранг матрицы не изменяется. Ч.т.д.

Если r(A)=r(B), то А и В – эквивалентные: А~В.

Теорема 5. При помощи элементарных преобразований можно привести матрицу к ступенчатому виду. Матрица называется ступенчатой, если она имеет вид:

А= 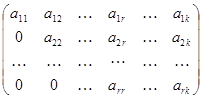, где a_ii≠0, i=1,2,…,r; r≤k.

Условия r≤k всегда можно достигнуть транспонированием.

Теорема 6. Ранг ступенчатой матрицы равен количеству ее ненулевых строк.

Т.е. Ранг ступенчатой матрицы равен r, т.к. есть отличный от нуля минор порядка r: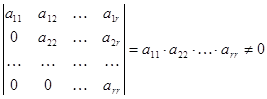

Дата добавления: 2015-08-27