Линейное свойство определителя.

Свойство антисимметрии при перестановке двух строк (столбцов).

При перестановке двух строк (столбцов) матрицы ее определитель меняет знак на противоположный.

Доказательство. Допустим сначала, что переставлены две соседние строки матрицы: i и i+1. Разложим определитель исходной матрицы Δ по элементам i-й строки, а определитель новой матрицы Δ^΄ - по элементам (i+1)-й строки. Разложения будут отличаться только знаком, т.к. в разложении определителя Δ^΄ каждое алгебраической дополнение A_i+1j будет иметь противоположный знак (множители (-1)^i+j сменятся на множители (-1)^i+1+j). Т.о. Δ^=-Δ^΄.

Если переставить не соседние строки, а, например, i-ю и (i+m)-ю, то эту перестановку можно рассматривать как последовательное смещение i-й строки на m строк вниз (при этом каждый раз знак определителя меняется), а (i+m)-й строки на (m-1) вверх и (m-1) раз меняется знак, т.е. знак поменяется нечетное число раз: (m+m-1=2m-1). Следовательно, Δ =-Δ^΄.

Для столбцов доказательство аналогично.

Линейное свойство определителя.

Некоторая строка а=(а₁,а₂,…,а_n) называется линейной комбинацией строк b=(b₁,b₂,…,b_n), c=(c₁,c₂,…,c_n),…, d=(d₁,d₂,…,d_n), с коэффициентами λ₁,λ₂,…,λ_k если она равна сумме произведений этих строк на эти числа:

a=λ₁b+λ₂c+…+λ_kd, т.е. a_j=λ₁b_j+λ₂c_j+…+λ_kd_j "j=1,2,…,n

Если в определителе n-го порядка D некоторая i-я строка (a_i1,a_i2,…,a_in) является линейной комбинацией строк (b_i1,b_i2,…,b_in) и (c_i1,c_i2,…,c_in) с коэффициентами l и m, то D=lD₁+mD₂, где D₁ – определитель, у которого i-я строка равна (b_i1,b_i2,…,b_in), а все остальные строки такие же, как и у D, а где D₂ – определитель, у которого i-я строка равна (с_i1,с_i2,…,с_in), а все остальные строки такие же, как и у D.

= +

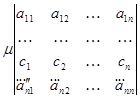
Доказательство. Разложим каждый из определителей D, D₁, и D₂ по i-й строке по формуле Δ=a_i1A_i1+a_i2A_i2+…+a_inA_in= . Заметим, что алгебраические дополнения A_ij i-й у всех 3-х определителей одинаковы. Следовательно, формула D=lD₁+mD₂ следует из равенств a_j=λb_j+mc_j "j=1,2,…,n ч.т.д.

Замечание. Линейное свойство справедливо и для случая, когда i-я строка является линейной комбинацией не 2-х, а нескольких строк.

Рассмотренные 3 свойства являются основными свойствами определителя. Следующие 5 свойств являются логическими следствиями этих свойств.

4. Определитель с двумя о динаковыми строками (столбцами), то равен 0.

Док-во. Переставим равные строки (столбцы) местами. С одной стороны, определитель не изменится, а с другой, по св-ву 2, поменяет знак. Т.е. Δ=-Δ, след-но, Δ=0.

Дата добавления: 2015-08-27