Поверхностные интегралы второго типа.

Пусть 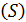некоторая двусторонняя гладкая (или кусочно-гладкая) поверхность, ограниченная кусочно-гладким контуром. Т.е. на этой поверхности мы различаем стороны и на каждой стороне имеем определённое направление обхода замкнутых контуров в качестве положительного, т.е. на каждой стороне имеется ориентация.

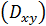Пусть на этой поверхности (т.е. в каждой точке поверхности) определена функция . Обозначим через проекцию заданной поверхности 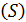на плоскость 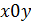. Разложим 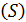сетью кусочно – гладких кривых на элементы 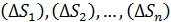. Выбрав в каждом элементе 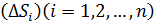произвольную точку 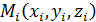, вычислим в этой точке значение функции R .

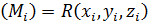Составим теперь для каждой стороны поверхности свою интегральную сумму, которые будут отличаться друг от друга знаком.

Именно, спроектировав разбиение 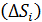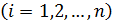на плоскость 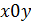, получим разбиение плоской области 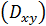на элементы 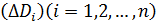. Каждый элемент 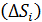и каждый элемент 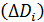имеют своё положительное направление обхода контура. Но когда мы обходим контур элемента 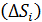в положительном направлении, проекция точки обхода тоже обходит контур 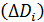. И это направление обхода может совпадать с положительным направлением обхода контура 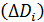, а может быть ему противоположно. Так, если мы рассматриваем элемент 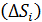принадлежащим верхней стороне поверхности 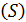, то положительное направление обхода его контура совпадёт с положительным направлением обхода контура 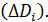Если же элемент 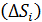брать принадлежащим нижней стороне поверхности 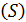, то положительное направление обхода контура 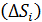будет противоположно положительному направлению обхода контура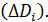

Составим свою интегральную сумму для каждой стороны поверхности 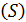по следующему правилу.

Если положительное направление обхода контура элемента 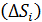соответствует положительному обходу контура его проекции 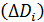, то умножим значение 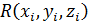, взятое в произвольной точке элемента 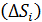, на площадь 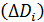. Если же положительное направление обхода контура 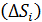будет соответствовать отрицательному обходу контура его проекции 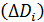, то умножим значение 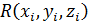, взятое в произвольной точке элемента 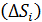, на площадь 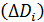, взятую со знаком «минус».

Придерживаясь сформулированного правила, составим интегральные суммы 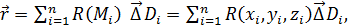где 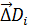подразумевает значение площади с соответствующим знаком.

Конечный предел таких интегральных сумм при бесконечном уплотнении разбиения поверхности 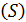, не зависящий ни от способа разбиения поверхности 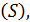ни от выбора точек 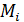в пределах каждой части 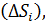называется поверхностным интегралом второго типа, распространенным на определенную сторону поверхности, и обозначается символом

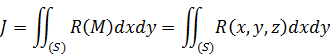
Впрочем, в этом символе не содержится указание на то, какую именно сторону поверхности имеют в виду, так что указание приходится делать всякий раз особо. Из самого определения следует, что интегралы, взятые по разным сторонам одной и той же поверхности, отличаются друг от друга знаком.

Пусть поверхность 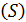задана уравнением 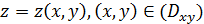, причем функция 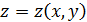непрерывна вместе со своими первыми частными производными.

Если интеграл берется по верхней стороне поверхности, то в интегральной сумме 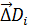, положительны, т.е. 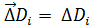. Подставляя в эту сумму вместе с 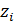, его значение 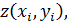приведем ее к виду:

.

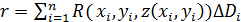Последнее выражение представляет собой интегральную сумму для обыкновенного двойного интеграла 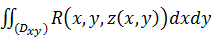. Приходя к пределу в равенстве 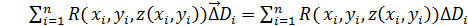, получим соотношение: .

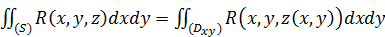Причем существование одного из этих интегралов влечет за собой существование другого. В частности они существуют, если подынтегральная функция непрерывна.

Если считать интеграл взятым по нижней стороне 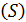, то с помощью аналогичных рассуждений получим

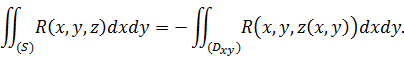
Вспоминая теперь формулы, выражающие поверхностные интегралы первого типа через двойные, и учитывая, что для верхней стороны поверхности 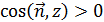, а для нижней 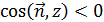, получим, что во всех случаях справедливо соотношение:

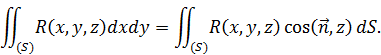
Подчеркнем, что поверхностный интеграл второго типа, взятый по верхней стороне поверхности, равен поверхностному интегралу первого типа с 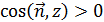, а поверхностный интеграл второго типа, взятый по нижней стороне поверхности, равен поверхностному интегралу первого типа с .

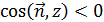Если вместо плоскости x 0 y проектировать поверхность 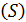на плоскость y 0 z или z 0 x, то получим два других поверхностных интеграла второго типа:

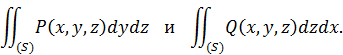
С учетом того, по какой стороне поверхности эти интегралы берутся, для них так же будут справедливы формулы, выражающие их через двойные интегралы:

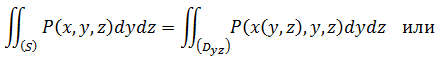
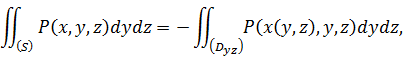
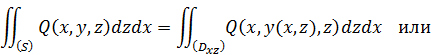
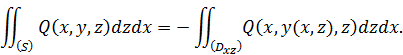
В силу формул, указанных в следствиях 2 и 3, будем иметь:

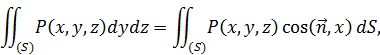
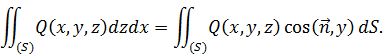
В приложениях чаще всего встречаются соединения интегралов всех видов: .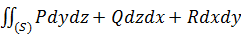

Соответственно, для такого выражения будет справедлива следующая формула: 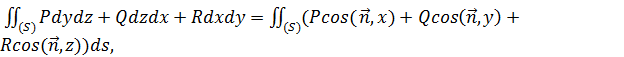сводящая поверхностный интеграл второго типа, к поверхностному интегралу первого типа.

Все определения и полученные результаты распространяются и на более общий случай поверхности – замкнутой или нет, - составленных из конечного числа простых незамкнутых гладких частей, примыкающих одна к другой, и в совокупности образующих двустороннюю поверхность.

Дата добавления: 2015-08-17