Формула остроградского-гаусса

Рассмотрим трехмерную пространственную область , ограниченную кусочно-гладкими поверхностями и цилиндрической поверхностью , образующие которой параллельны оси z.

Направляющей поверхности служит кусочно-гладкая замкнутая кривая на плоскости x 0 y, ограничивающая плоскую область ( – проекция на x 0 y). В частном случае на кривой может выполняться и равенство , тогда вырождается в линию.

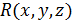Допустим, что в области определена функция непрерывная вместе со своей производной во всей , включая ее границу. Имеем для тройного интеграла в области :

Если ввести в рассмотрение поверхностные интегралы, то в силу установленных формул:

причем первый из интегралов справа распространен на верхнюю сторону поверхности , а второй на нижнюю сторону поверхность . Равенство не нарушится, если мы прибавим к правой части интеграл , распространенный на внешнюю сторону поверхности , так как он равен нулю.

Объединяя все поверхностные интегралы, получим формулу:

где – внешняя нормаль к области на ее поверхности.

Эти формулы установлены нами лишь для цилиндрических брусов, определенным образом ориентированных. Но они верны и для гораздо более широкого класса тел, которые могут быть разложены на части изученного вида с помощью цилиндрических поверхностей с образующими, параллельным оси z. Действительно, осуществив это разложение, мы можем применить к каждой части формулу (*) и затем сложить результаты. Так как интегралы, распространенные на вспомогательные цилиндрические поверхности равны нулю, мы снова приходим к формуле (*).

Можно доказать, что (*) справедлива вообще для тел, ограниченных произвольными кусочно-гладкими поверхностями.

Аналогично (*) имеют место формулы:

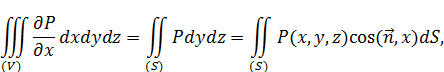
если функции P и Q непрерывны в области вместе со своими производными и .

Сложив все три формулы, придем к формуле Остроградского-Гаусса:

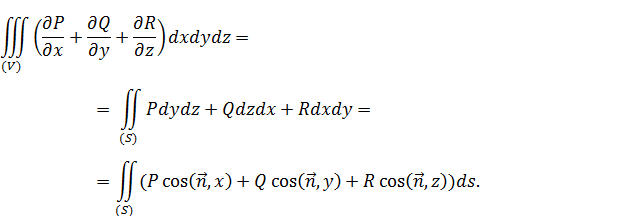
Взяв P=x, Q=y, R=z, получим три формулы для объема тела:

Сложив эти формулы, получим:

Дата добавления: 2015-08-17