Сторона поверхности

В ряде случаев это понятие интуитивно ясно. Если поверхность задается явным уравнением вида 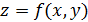, можно говорить о верхней или нижней стороне поверхности, подразумевая, что ось 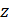направлена вверх. Если поверхность ограничивает тело, то также легко представить себе её две стороны – внутреннюю и внешнюю.

Рассмотрим гладкую поверхность 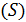, замкнутую или ограниченную кусочно-гладким контуром. Взяв на поверхности определенную точку 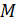, проведём в ней нормаль, которой припишем определённое направление – одно из двух возможных (они отличаются одно от другого знаками направляющих косинусов). Проведём на поверхности замкнутый контур, исходящий из 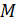и возвращающийся в 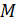, причём предположим, что контур не пересекает границы поверхности. Заставим точку 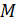обойти этот контур и в каждом из последовательных её положений будем приписывать нормали то из двух направлений, в которое непрерывно переходит направление, выбранное нами в начальном положении 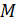. При этом может случиться одно из двух: либо после обхода контура мы вернёмся в точку 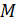с тем же направлением нормали, либо же с направлением, противоположному исходному.

Если найдётся такая точка и такой контур, что после его обхода мы вернёмся к исходной точке с противоположным направлением нормали, то такая поверхность называется односторонней. Классическим примером такой поверхности является поверхность Мёбиуса.

Мы такие поверхности рассматривать не будем.

Предположим теперь, что какова бы не была точка 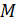и каков бы ни был замкнутый контур, проходящий через 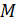и не пересекающий границы поверхности, после обхода его мы неизменно возвращаемся в исходную точку 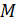с исходным направлением нормали. При этих условиях поверхность называется двусторонней.

Пусть 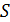– двусторонняя поверхность. Возьмём на ней любую точку 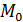и припишем нормали в этой точке определённое направление. Взяв какую – либо другую точку 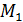поверхности, соединим 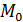и 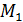произвольным путём , лежащим на поверхности и не пересекающим её границы. Заставим точку 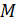перейти из 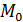в 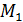по этому пути. Если при этом непрерывно изменять направление нормали, то точка 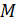придёт в положение 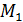с вполне определённым направлением нормали, не зависящем от выбора пути . Действительно, если бы, придя в точку 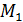из 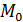по двум различным путям 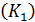и 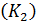, мы получили бы в точке 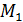различные (противоположные) направления нормали, то замкнутый путь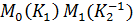 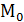привёл бы нас в точку 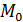с направлением нормали, отличным от исходного, что противоречило бы двусторонней поверхности.

Таким образом, на двусторонней поверхности выбор направления нормали в одной точке однозначно определяет выбор направления нормали во всех точках поверхности.

Совокупность всех точек поверхности с указанными направлениями нормалей и называется определённой стороной поверхности.

Пусть поверхность задана явным уравнением 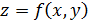в предположении, что частные производные 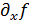и 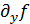непрерывны. В этом случае направляющие косинусы имеют выражения:

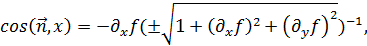
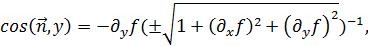
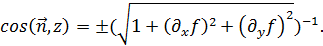
Выбрав перед радикалом определённый знак, мы тем самым устанавливаем во всех точках поверхности определённое направление нормали. В силу сделанных предположений, направляющие косинусы будут непрерывными функциями и положение (направление) нормали будет также непрерывно зависеть от положения точки. Отсюда ясно, что выбор знака перед радикалом в формулах для косинусов определяет сторону поверхности в том именно смысле, какой выше приписан этому понятию.

Если выберем знак +, то во всех точках поверхности 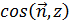будет положительным, т.е. угол, составленный с осью 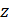нормалью соответствующей стороне, будет острым. Таким образом, сторона поверхности, определяемая указанным выбором знака, оказывается верхней стороной.

Дата добавления: 2015-08-17