Формула Стокса

Пусть задана гладкая поверхность 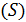, ограниченная гладким контуром . Предполагаем, что прямые, параллельные оси 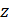, пересекают 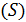только в одной точке. Обозначим через проекцию 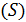на плоскость . Проекцию линии обозначим . Контур ограничивает область . Направление нормали к 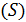берём так, чтобы оно составляло острый угол с осью 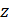, так что . Примем, что поверхность задана явным уравнением 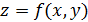. Направляющие косинусы на выбранной верхней стороне поверхности 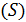имеют вид

; ; .

Отсюда следует .

Пусть в каждой точке поверхности 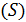определена функция , а также определены все её частные производные , , , причём как сама функция , так и все её частные производные предполагаются непрерывными на 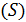вплоть до её границы . Рассмотрим криволинейный интеграл по кривой :

Линия лежит на 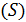и, пользуясь уравнением этой поверхности, мы можем заменить под знаком интеграл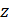а на 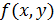. При этом подынтегральная функция , будет зависеть только от 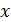и . Так как линия является проекцией линии , то координаты точки на такие же, как у точки на , а поэтому интегрирование по (L) можно заменить интегрированием по :

Применим к этому интегралу формулу Грина с , т.е.

Пользуясь формулой, указанной в Следствии 1, приведём интеграл по плоской области к интегралу по поверхности 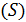. В результате получим

Заменив 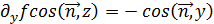и переставив слагаемые в правой части последнего равенства, получим

Эта формула введена в предположении, что прямые, параллельные оси 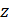пересекают 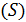не более чем в одной точке. Если это не так, то разбиваем 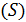на части вспомогательными линиями так, чтобы каждая часть удовлетворяла такому условию. К каждой отдельной части формула применима.

Складывая полученные таким образом для всех частей формулы, будем иметь слева интеграл по контуру , так как интегралы по вспомогательным контурам будут браться два раза в противоположных направлениях и уничтожаться. Справа получим двойной интеграл по всей поверхности 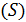, т.е. формула справедлива в общем случае.

Аналогичным образом можно установить две другие формулы

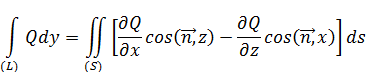
Складывая три полученные формулы, придём к формуле Стокса:

С использованием формул, связывающих поверхностные интегралы первого и второго типов, формулу Стокса можно записать так:

При пользовании этой формулой надо иметь в виду, что выбирается определённая сторона поверхности и с этим выбором согласуется обход контура .

ЛИТЕРАТУРА

1. В.А. Ильин, В.А. Свешников, Б.Х. Сендов. Математический анализ. МГУ, 1985.

2. Л.Д. Кудрявцев. Краткий курс математического анализа. М, «Наука», 1989.

3. Л.Д. Кудрявцев. Математический анализ. М., «Высшая школа», 1981, т.1,2.

4. В.А. Ильин, Э.Г. Поздняк. Основы математического анализа. М., «Наука», 1982, ч. 1,2.

5. И.И. Баврин. Курс высшей математики. М., Просвещение, 1992.

6. С.М. Никольский, Я.С. Бугров. Высшая математика. Дифференциальное и интегральное исчисление. М., «Наука», 1984.

7. А.Ф. Берман. И.Г. Араманович. Краткий курс математического анализа. М., «Наука», 1979.

8. Н.С. Пискунов. Дифференциальное и интегральное исчисление для ВТУЗов. М. «Наука», 1979.

9. И.М. Уваренков. М.З. Маллер. Курс математического анализа. М. «Просвещение», 1976, т.2.

10. Г.М. Фихтенгольц. Курс дифференциального и интегрального исчисления. М. «Наука», 1966, т.2 и т.3.

11. Г.Н. Берман. Сборник задач по курсу математического анализа. М. «Наука», 1980.

12. Л.А. Кузнецов. Сборник заданий по высшей математике. Т.Р. М. «Высшая школа», 1983.

13. Г.И. Запорожец. Руководство к решению задач по математическому анализу. М. «Высшая школа», 1974.

14. В.П. Демидович. Задачи и упражнения по математическому анализу. М. «Наука», 1980.

15. И.А. Виноградова, С.Н. Олейник, В.А. Садовничий. Математический анализ в задачах и упражнениях. М. Издательство Московского университета, 1991.

16. Л.Г. Лелёвкина, Р.Р. Рафатов. Методическое руководство к решению задач и контрольных заданий по кратным и криволинейным интегралам. Кыргызско – Российский Славянский университет. Бишкек. 1997.

17. Р.Р. Рафатов. Методические разработки по курсу высшей математики. Раздел «Элементы теории поля». – ФПИ. Фрунзе, 1988.

Дата добавления: 2015-08-17