
Читайте также:
|
Пусть в плоскости x 0 y задана область  , ограниченная замкнутым контуром
, ограниченная замкнутым контуром  . Предположим, что прямые, параллельные осям x и y пересекают этот контур не более чем в двух точках, так что контур можно описать любым из следующих двух способов:
. Предположим, что прямые, параллельные осям x и y пересекают этот контур не более чем в двух точках, так что контур можно описать любым из следующих двух способов:
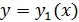 , ,  , ,
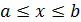
| 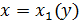 , x , x 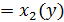 , ,

| |||||||||||||||||
|
Пусть в области  заданы функции P и Q, непрерывные вместе со своими частными производными первого порядка.
заданы функции P и Q, непрерывные вместе со своими частными производными первого порядка.
Рассмотрим интеграл 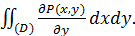
Представляя его в виде двукратного получим:
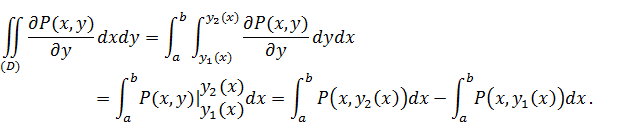
Интегралы в правой части последнего выражения являются криволинейными интегралами, взятыми соответственно по верхней: 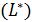 и нижней
и нижней  частям контура
частям контура  . Но только направление обхода контуров у этих интегралов различное. Для того, что бы у обоих интегралов было одно направление обхода контура, переменим в первом из них направление интегрирования.
. Но только направление обхода контуров у этих интегралов различное. Для того, что бы у обоих интегралов было одно направление обхода контура, переменим в первом из них направление интегрирования.
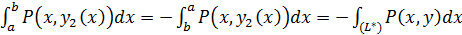 . Отсюда следует:
. Отсюда следует:
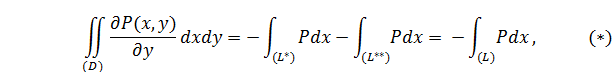
причем контур обходиться против часовой стрелки.
Аналогично
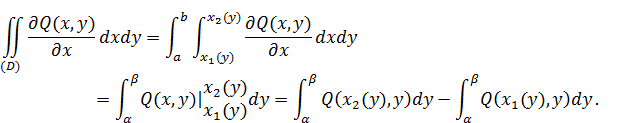
Здесь для сохранения правила обхода против часовой стрелки нужно изменить порядок интегрирования во втором интеграле справа. Тогда по аналогии получим:
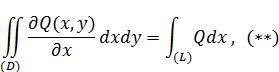
Вычитая (*) из (**) получим формулу Грина:
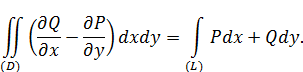
ЗАМЕЧАНИЕ. Каждая из формул (*) и (**) дает соответствующую формулу интегрирования по частям.
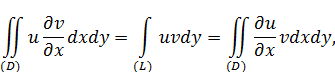

Дата добавления: 2015-08-17; просмотров: 40 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| ФОРМУЛА ИНТЕГРИРОВАНИЯ ПО ЧАСТЯМ | | | ФОРМУЛА СТОКСА |