Орентация поверхности.

Пусть 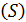будет незамкнутая гладкая двусторонняя поверхность, ограниченная простым контуром . Выберем определённую сторону этой поверхности. Припишем теперь контуру определённое направление обхода в качестве положительного по следующему правилу: обход должен казаться происходящим против часовой стрелки наблюдателю, движущему в этом направлении по контуру так, что нормаль к поверхности, отвечающая выбранной стороне, пронизывает его от ног к голове.

Слова «против часовой стрелки» означают, точнее говоря, что наблюдатель должен видеть непосредственно прилегающую к нему часть поверхности слева от себя. По этому же правилу одновременно устанавливается положительное направление обхода для каждого простого замкнутого контура, лежащего на поверхности и ограничивающего некоторую её часть. Только с этой частью и надлежит считаться при определении положительного направления на контуре.

Направление обхода, обратное положительному, называется отрицательным. В совокупности всё это и составляет содержание понятия ориентация поверхности.

Если исходить из другой стороны поверхности, то нормали изменят своё направление на обратное, изменится положение наблюдателя, в связи с чем переменится положительное и отрицательное направление обхода контура и других контуров, лежащих на поверхности.

Поверхность изменит свою ориентацию.

Таким образом, если всегда держаться установленного правила, выбор стороны поверхности определит её ориентацию и, обратно, выбор положительного направления обхода контура поверхности однозначно определит её сторону.

В случае замкнутой гладкой поверхности 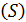, ограничивающей некоторое тело, речь может идти о внешней или о внутренней по отношению к этому телу стороне поверхности. Установить для любого просто замкнутого контура положительное направление обхода с помощью сформированного выше правила на этот раз не удаётся. Причина этого – двоякая. Прежде всего, такой контур может просто «не разделять» поверхность (как, например, в случае любых параллелей или меридианов на торе), и тогда поверхность примыкает к контуру с обеих сторон. Но если даже контур «разделяет» поверхность на две области, то он обе их «ограничивает» в равной мере, и в зависимости от того, какую из областей выбрать, наше правило приводит к тому или другому из двух направлений на контуре, как к положительному. Ограничиваясь контурами, «разделяющими» поверхность, мы станем вместе с контуром указывать и область, тогда положительное направление устанавливается уже вполне однозначно. Этим и определяется ориентация поверхности – та или другая, в зависимости от выбранной стороны.

В случае кусочно-гладкой поверхности 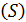, состоящей из гладких кусков , ,…, примыкающих один к другому по ребру, предположим прежде всего, что каждый из этих кусков в отдельности является двусторонней поверхностью.

Но этого недостаточно для того, чтобы всю поверхность 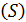можно было рассматривать как двустороннюю; ведь и поверхность Мёбиуса легко состаляется из двух гладких двусторонних кусков.

На контуре каждого куска выберем в качестве положительного направления одно из двух направлений. Если этот выбор можно произвести так, чтобы всегда общая часть двух примыкающих контуров описывалась в противоположных направлениях, то тогда поверхность 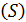называется двусторонней.

Если хоть в одном случае направление обхода контура заменить на противоположное, то для соблюдения сформулированного условия придётся то же сделать и со всеми контурами. Тогда и выбранные стороны всех кусков заменятся противоположными; их совокупность составит вторую сторону поверхности.

Дата добавления: 2015-08-17