Студопедия
Случайная страница | ТОМ-1 | ТОМ-2 | ТОМ-3
АрхитектураБиологияГеографияДругоеИностранные языки
ИнформатикаИсторияКультураЛитератураМатематика
МедицинаМеханикаОбразованиеОхрана трудаПедагогика
ПолитикаПравоПрограммированиеПсихологияРелигия
СоциологияСпортСтроительствоФизикаФилософия
ФинансыХимияЭкологияЭкономикаЭлектроника

Формула интегрирования по частям

ОПРЕДЕЛЕНИЕ НАПРАВЛЯЮЩИХ КОСИНУСОВ НОРМАМИ | ПЛОЩАДЬ ПОВЕРХНОСТИ | СТОРОНА ПОВЕРХНОСТИ | ОРЕНТАЦИЯ ПОВЕРХНОСТИ. | ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ ПЕРВОГО ТИПА | ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ ВТОРОГО ТИПА. | ФОРМУЛА СТОКСА | ЗАДАНИЯ |


Читайте также:
  1. Божья формула успеха
  2. Валерий Синельников » Языкознание » Таинственная сила слова. Формула любви. Как слова влияют на нашу жизнь » стр. 10
  3. Валерий Синельников » Языкознание » Таинственная сила слова. Формула любви. Как слова влияют на нашу жизнь » стр. 11
  4. Валерий Синельников » Языкознание » Таинственная сила слова. Формула любви. Как слова влияют на нашу жизнь » стр. 12
  5. Валерий Синельников » Языкознание » Таинственная сила слова. Формула любви. Как слова влияют на нашу жизнь » стр. 3
  6. Валерий Синельников » Языкознание » Таинственная сила слова. Формула любви. Как слова влияют на нашу жизнь » стр. 4
  7. Валерий Синельников » Языкознание » Таинственная сила слова. Формула любви. Как слова влияют на нашу жизнь » стр. 5

Переобозначим координаты 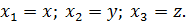Для любых непрерывно дифференцируемых функций u и v справедлива формула:

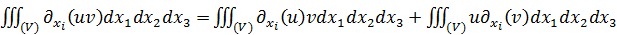. Отсюда следует . Обозначим также . Пользуясь установленными ранее формулами, получим

Пользуясь введенными обозначениями координат и введя так же обозначения:

можем переписать формулу Остроградского-Гаусса в следующем виде:

так как .

 

Дата добавления: 2015-08-17; просмотров: 85 | Нарушение авторских прав

<== предыдущая страница | следующая страница ==>
ФОРМУЛА ОСТРОГРАДСКОГО-ГАУССА| ФОРМУЛА ГРИНА
mybiblioteka.su - 2015-2024 год. (0.007 сек.)