Смачивание жидкостью твердой поверхности. Краевой угол смачивания

На границе раздела трех фаз наблюдаются сложные соотношения между межфазными поверхностными натяжениями, которые обусловливают явления, актуальные для современной технологии, такие как смачивание и растекание, капиллярные явления, растворение твердого тела.

Смачивание –явление, заключающееся во взаимодействии жидкости с твердым или другим жидким телом при наличии одновременного контакта трех несмешивающихся фаз.  

Степень смачивания определяет форму капли жидкости на твердой поверхности.

Мерой смачивания обычно служит краевой угол или угол смачивания q – угол между смачиваемой поверхностью и поверхностью жидкости по периметру смачивания.

Рассмотрим кратко явления смачивания и понятие краевого угла смачивания на примере капли жидкости, нанесенной на поверхность другого тела (рис. 3.12).

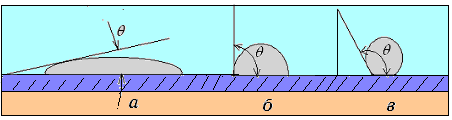
Рис. 3.12. Различные случаи неполного смачивания

а – q < 90⁰; б – q = 90⁰; в – q > 90⁰

В зависимости от значений равновесного краевого угла различают три основных вида смачивания:

1. Молекулы жидкости взаимодействуют с молекулами твердого тела сильнее, чем между собой. Жидкость растекается по поверхности или, как говорят, смачивает ее. Растекание происходит до тех пор, пока жидкость не покроет всю поверхность твердого тела (образование мономолекулярного слоя). Это случай полного смачивания.

2. Молекулы жидкости взаимодействуют друг с другом значительно сильнее, чем с молекулами твердого тела, растекания не произойдет. Пример – нанесение капли ртути на любую неметаллическую поверхность.

3. Между этими двумя крайними случаями возможны переходные случаи неполного смачивания (рис.3.12), когда капля образует с поверхностью твердого тела определенный равновесный угол, называемый краевым углом или углом смачивания.

Краевой угол, образуемый каплей на поверхности твердого тела, всегда измеряется со стороны жидкости. Полного несмачивания (q = 180⁰) практически никогда не наблюдается, так как между жидкостью и твердым телом всегда действуют силы притяжения, хотя бы и очень малые.

Приведем значения краевого угла, образуемого водой на поверхности различных твердых тел в атмосфере воздуха:

Кварц	Малахит	Галенит	Графит	Тальк	Сера	Парафин
			55-60

Смачивание жидкостью твердого тела можно объяснить как результат действия сил поверхностного натяжения.

Рассмотрим пример неполного смачивания (рис. 3.13). Окружность капли является границей взаимодействия трех сред – жидкости 1, воздуха 2, твердого тела 3.

Рис. 3.13. Смачивание на границе трех фаз (по Ребиндеру): 1 – жидкость; 2 – воздух; 3 – твердая поверхность

Эти среды имеют разграничивающие их поверхности: 1) поверхность жидкость – воздух с поверхностным натяжением s_1,2; 2) поверхность воздух – твердое тело с поверхностным натяжением s_2,3; 3) поверхность жидкость – твердое тело с поверхностным натяжением s_1,3.

При образовании равновесного краевого угла q все три силы должны уравновешивать друг друга.

Условие равновесия соприкасающихся фаз выразится уравнением Юнга:

s_2,3 = s_1,3 + s_1,2 cosq.

Величина cosq связана с межфазными поверхностными натяжениями соотношением:

Величину cos q, характеризующую способность жидкости смачивать поверхность, называютсмачиваниеми обозначают через В.

При полном смачивании краевой угол смачивания q = 0^о; В = +1.

При полном несмачивании краевой угол смачивания q =180^о; В = –1.

Характер смачивания жидкостью твердой поверхности определяется соотношением молекулярных взаимодействий в твердой и жидкой фазах и между фазами. Характеристиками этих взаимодействий являются значения удельных свободных поверхностных энергий на границах раздела твердое тело – газ s_2,3, жидкость – газ s_1,2 и твердое тело – жидкость s_1,3.

Если s_1,3 < s_2,3, то q < p/2. В этом случае жидкость имеет вогнутый мениск (хорошо смачивает поверхность твердого тела).

Если s_1,3 > s_2,3, то q > p /2. При этом жидкость имеет выпуклый мениск (плохо смачивает поверхность).

Чем меньше угол q и соответственно больше cosq = В, тем лучше смачивание.

Так как жидкость тем лучше смачивает твердое тело, чем меньше взаимодействие между ее молекулами, неполярные жидкости с малым поверхностным натяжением обычно хорошо смачивают поверхность.

Так, углеводороды с s = (20 – 30)·10^–3 Н/м практически смачивают все твердые тела, вода с s = 72,75·10^–3 Н/м (при t = 20^оС) смачивает лишь некоторые тела, например, стекло, кварц, неорганические соли; ртуть с s = 475 ·10^–3 Н/м смачивает только некоторые металлы.

Изучение избирательного смачивания в системе вода – жидкий углеводород – твердая поверхность дает характеристику гидрофильности и гидрофобности (олеофильности) поверхности:

при q < 90^oповерхность является гидрофильной,

при q > 90^o– гидрофобной (олеофильной).

Изменение смачиваемости (гидрофилизация или гидрофобизация) поверхности возможно как при предварительной адсорбции ПАВ из раствора, так и при растворении ПАВ в жидкости, контактирующей с твердой поверхностью.

Смачивание и краевой угол смачивания очень сильно зависят от микрорельефа поверхности, и краевой угол смачивания будет иметь отклонения от значения, которое определяется распределением сил. Краевой угол смачивания и его отклонение от рассчитанного значения можно определить экспериментально с учетом шероховатости поверхности.

Дата добавления: 2015-08-20