Капиллярная конденсация

В различных процессах, связанных со смачиванием, важную роль играет капиллярное давление, которое возникает из-за искривления поверхности жидкости.

Между искривленной и плоской поверхностью раздела существует разность давлений, которая называется капиллярным давлением. Для пояснения физического смысла капиллярных явлений проведем качественное их рассмотрение на примере мыльного пузыря. Если в процессе выдувания пузыря открыть конец трубочки, то пузырь, находящийся на другом конце, начнет уменьшаться в размерах и втянется в трубку. Поскольку в этом обратном процессе воздух внутри пузыря сообщается с атмосферой, то для поддержания равновесного состояния давление изнутри должно быть больше внешнего.

Если в данном опыте соединить трубку с манометром, то он зарегистрирует избыточное давление в объемной фазе газа с вогнутой стороны поверхности пузыря. Найдем количественную зависимость между ним и кривизной поверхности. Воспользуемся для этого термодинамическим выражением для изменения энергии Гельмгольца, полученным ранее.

Рассмотрим две контактирующие фазы a и b, разделенные искривленной поверхностью. В состоянии равновесия возможны вариации площади поверхности ds и объема dV без изменения числа молей dn в системе. Таким образом, в нашем случае dn = 0и dT = 0.

В соответствии с последним уравнением для рассматриваемой системы можно записать

Исходя из равенства:

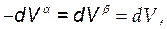получаем

где dF = 0, так как система находится в равновесии.

Отсюда находим

Предположим, что поверхность имеет сферическую форму. Тогда

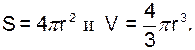
С учетом этого получаем уравнение Лапласа:

Искривление поверхности характеризуют радиусом кривизны r, направленным внутрь жидкости при выпуклой поверхности и наружу при вогнутой поверхности. В общем случае, для несферических поверхностей, уравнение Лапласа имеет следующий вид:

где r₁, r₂ – главные радиусы кривизны; DР называют капиллярным давлением.

При опускании тонкого стеклянного капилляра в воду (рис. 3.14, а) краевой угол смачивания близок к нулю и мениск вогнутый. Давление р при этом ниже, чем давление при плоской поверхности. В результате мениск поднимается на высоту h, при которой вес поднятого столба жидкости уравновешивает разность давлений между обеими поверхностями. При погружении капилляра в несмачиваемую жидкость, напротив, происходит опускание уровня жидкости в капилляре (рис. 3.14, б).

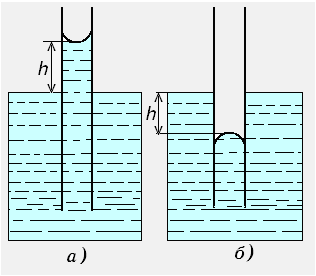
Рис. 3.14. Капиллярное поднятие (а) и опускание (б) жидкости

Изменение давления пара над искривленной поверхностью по сравнению с плоской определяется уравнением Кельвина–Томсона. Оно получается из условия равенства химических потенциалов в смежных фазах, находящихся в состоянии термодинамического равновесия.

где s – поверхностное натяжение конденсированной жидкости; р, р_s – давления насыщенного пара над сферическими каплями жидкости и плоской поверхностью; V_m – молярный объем; r_s – радиус средней кривизны поверхности раздела фаз.

В соответствии с данным уравнением, давление насыщенного пара вблизи искривленной и плоской поверхностями не одинаково. В уравнение входят кривизна поверхности (1/r) и поверхностное натяжение s. Видно, что, чем больше кривизна, тем больше относительная разница давлений пара. Она возрастает также при увеличении поверхностного натяжения s. Известно, что выпуклая поверхность имеет положительную кривизну (знак “+”), вогнутая – отрицательную (знак “–”). Поэтому, исходя из уравнения, можно заключить, что над выпуклой поверхностью давление пара больше, чем над плоской; над вогнутой же – меньше. Следствием этого является то, что в тонкодисперсных адсорбентах капиллярного типа конденсация паров влаги протекает значительно раньше, чем на плоской поверхности.

В результате на плоских поверхностях конденсация начинается при давлении насыщения р_нас, а в узких капиллярах тонкопористых адсорбентов давление насыщенного пара будет ниже, чем над плоской поверхностью и пар в капилляре, не достигнув давления насыщения, уже пересыщен и конденсируется при р_s < р_нас. Этот процесс называется капиллярной конденсацией. При наличии капиллярной конденсации изотерма адсорбции при давлении насыщенного пара круто поднимается вверх (рис. 3.15).

Рис. 3.15. Изотерма адсорбции при капиллярной конденсации

Положение кривой зависит от характера пор адсорбента. Любая капиллярная конденсация начинается с адсорбции и идет по законам адсорбции, а заканчивается процессами конденсации. Капиллярная конденсация наблюдается только на вогнутых поверхностях, если адсорбат смачивает стенки капилляра адсорбента. Чем больше кривизна поверхности, тем меньше давление конденсации.

Дата добавления: 2015-08-20