Читайте также:
|
Если в задаче В9 на ЕГЭ по математике вам надо просто посчитать объем конуса или площадь сферы — считайте, что повезло. Применяйте формулы объема и площади поверхности цилиндра, конуса и шара. Все они есть в нашей таблице.
В некоторых задачах В9, кроме формул, нужна еще и элементарная логика. Например, если линейные размеры тела вращения уменьшились в два раза — его площадь поверхности уменьшится в 4, а объем — в 8 раз (ведь 2?=4, 2?=8). Как, например, в этой задаче. Как и остальные, она взята из банка заданий ФИПИ.
1. Объем конуса равен 16. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
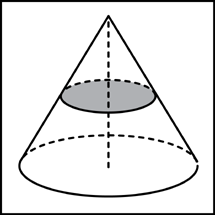
Очевидно, что объем меньшего конуса в 8 раз меньше объема большого и равен двум.
Для решения некоторых задач полезны хотя бы начальные знания стереометрии. Например — что такое правильная пирамида или прямая призма. Полезно помнить, что у цилиндра, конуса и шара есть еще общее название — тела вращения. Что сферой называется поверхность шара. А, например, фраза «образующая конуса наклонена к плоскости основания под углом 30?» предполагает, что вы знаете, что такое угол между прямой и плоскостью. Вам также может пригодиться теорема Пифагора и простые формулы площадей фигур.
Иногда неплохо нарисовать вид сверху. Или, как в этой задаче, — снизу.
2. Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду?
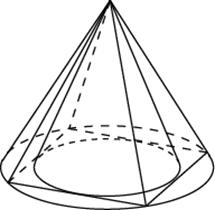
Всё просто — рисуем вид снизу. Видим, что радиус большего круга в 
раз больше, чем радиус меньшего. Высоты у обоих конусов одинаковы. Следовательно, объем большего конуса будет в 2 раза больше.
Еще один важный момент. Помним, что в задачах части В вариантов ЕГЭ по математике ответ записывается в виде целого числа или конечной десятичной дроби. Поэтому никаких или? у вас в ответе в части В быть не должно. Подставлять приближенное значение? тоже не нужно! Помните, что оно обязательно должно сократиться. Именно для этого в некоторых задачах задание формулируется, например, так: «Найдите площадь боковой поверхности цилиндра, деленную на?».
А где же еще применяются формулы объема и площади поверхности тел вращения? Конечно же, в задаче С2. Мы тоже расскажем о ней, потому что это наиболее доступная задача из части С.
Дата добавления: 2015-08-17; просмотров: 135 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Геометрический парадокс: катет равен гипотенузе! | | | Большая масса кирпичной кладки требует массивный фундамент. |