
Читайте также:
|
Сейчас я вам докажу, что катет равен гипотенузе.
И рисую новый чертёж, с новым «доказательством».
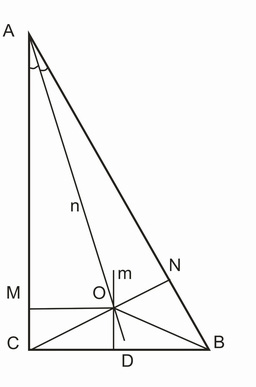
Построим прямоугольный треугольник АВС, угол С равен 90 градусов.
Пусть точка D — середина ВС.
Проведем лучи n — биссектрису угла А, и m — серединный перпендикуляр к ВС.
Лучи n и m пересекаются в точке О.
Опустим из точки О перпендикуляры на стороны АВ и АС. Точки М и N — основания этих перпендикуляров.
Рассмотрим треугольники АМО и АNО.
Они равны, так как оба они — прямоугольные, угол МАО равен углу NAO (по построению), гипотенуза АО —общая. Следовательно, ОМ = ON, AM = AN.
Рассмотрим треугольники СОD и OBD. Они равны, так как ОD — серединный перпендикуляр к ВС (по построению), то есть медиана и высота треугольника СОВ. Следовательно, ОС = ОВ.
Рассмотрим треугольники МСО и NBO. Они оба — прямоугольные, ОС = ОВ, ОМ = ON (по доказанному),
следовательно, треугольник МСО равен треугольнику NBO, и поэтому МС = NB.
Ну а дальше всё просто:-)
Как мы уже доказали, МС = NB, AM = AN. Следовательно,
МС + AM = NB + AN,
АС = АВ, катет равен гипотенузе, что и требовалось доказать:-)
Всё повторяется — но на этот раз ребятам всё-таки уже проще отстаивать собственное мнение, проще строить настоящее доказательство, основанное не на эмоциях, а на знаниях.
Может быть, в этом и ответ на вопрос: «Зачем учить геометрию».
Не только для того, чтобы не просчитаться с покупкой рулонов обоев! Кроме практической пользы, в геометрии есть особый смысл. Логическое мышление — один из путей к независимости личности.
Научной и нравственной основой курса геометрии является принцип доказательности всех утверждений. И
это единственный школьный предмет, включая даже предметы математического цикла, полностью основанный на
последовательном выводе всех утверждений. Людьми, понимающими, что такое доказательство, трудно и даже
невозможно манипулировать.
Из статьи И.Ф.Шарыгина «Нужна ли школе 21-го века Геометрия»
Впрочем, если вы всё ещё считаете, что геометрия вам не нужна — это ваш выбор. Вам будут продавать столько рулонов обоев (и всего остального), сколько посчитают нужным:-)
Дата добавления: 2015-08-17; просмотров: 296 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Геометрия: с нуля до группы С | | | Формулы объема и площади поверхности. Цилиндр, конус и шар |