Читайте также:
|
Дано: <ABC- вписанный
Доказать, что
Доказательство:
1 случай. Пусть центр окружности лежит на стороне
вписанного угла.
Соединим точки А и О. Треугольник АОВ –
равнобедренный, т.к АО=ОВ как радиусы одной
окружности, значит, <1=<2
Угол АОС – внешний для треугольника АОВ, поэтому
<AOC=<1+<2 (по теореме о внешнем угле).
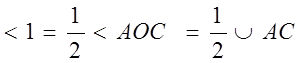<AOC=2<1. Но угол АОС – центральный и он равен дуге, на которую опирается, значит
Т.е
2 случай. Пусть центр окружности лежит вне вписанного угла.
Доказать, что
Доказательство:
3 случай. Пусть центр окружности лежит внутри вписанного угла.
Доказать, что
|
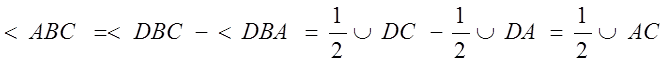
Доказательство:
Дата добавления: 2015-08-17; просмотров: 127 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Тангенсом острова угла прямоугольного треугольника называется отношение синуса к косинусу этого угла | | | О ПРЕДМЕТЕ ЛОГИКИ |