Квадратом называется прямоугольник, у которого все стороны равны.

Свойства квадрата

1) Диагонали квадрата равны

2) Диагонали квадрата перпендикулярны

3) Диагонали квадрата являются биссектрисами

его углов

Билет 7. Площадь прямоугольника. Площадь параллелограмма (доказательство теоремы о площади параллелограмма)

Площадь прямоугольника.

Теорема. Площадь прямоугольника равна произведению двух его смежных сторон.

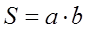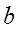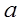Площадь параллелограмма.

Теорема. Площадь параллелограмма равна произведению его основания на высоту.

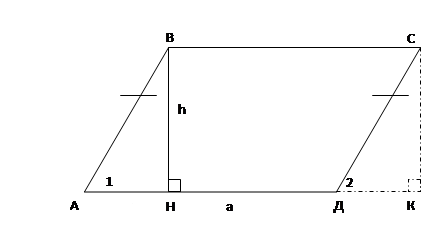
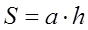Дано: АВСД – параллелограмм, а- основание, h- высота, провед1нная к основанию

Доказать:

Доказательство:1)проведём CK АД

BCHK-прямоугольник

2)Докажем, что S ABCD=S HBCK

3)S ABCD=S ABH+S BCDH

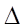
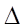S HBCK=S DKC+S BCDH

ABH= DCK (по гип. и острому углу, т.к AB=CD (по 1 свойству пар-ма),

1= 2 (как соответственные)

4) Значит S ABH=S DCK, значит S ABCD=S HBCK

S HBCK=BC*h=a*h, значит S ABCD=a*h

Билет 8. Площадь треугольника.(с доказательством)

Теорема. Площадь треугольника равна половине произведения его основания на высоту.

Доказать: 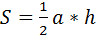(а – основание АС, h- высота ВH, проведённая к основанию)

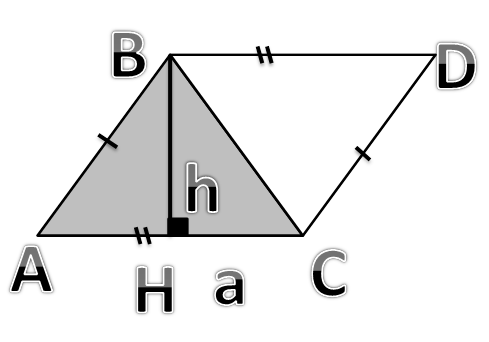
Док-во:

1. Достроим треугольник АВС до параллелограмма АВСД.

2. 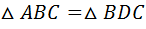(по 3 сторонам), значит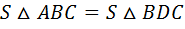

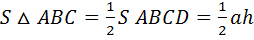
Билет 9. Площадь ромба. Площадь трапеции (доказательство одной теоремы на выбор)

Теорема Площадь ромба равна половине произведения его диагоналей

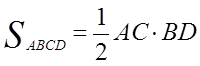
Дано: АВСД- ромб, АС и ВД- его диагонали

Доказать:

Доказательство:

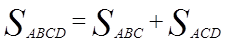
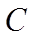
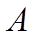
Площадь ромба равна сумме площадей двух треуголь-

ников:

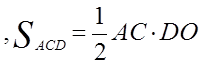
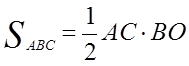Площадь треугольника равна половине произведения основания

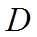на высоту, т.е

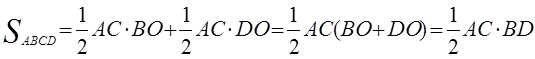
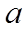Теорема. Площадь трапеции равна произведению полусуммы её оснований на высоту.

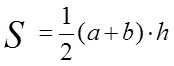
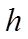
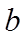
Билет 10. Теорема Пифагора.(с доказательством)

Теорема Пифагора Квадрат гипотенузы прямоугольного треугольника равен сумме квадратов его катетов.

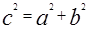
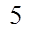
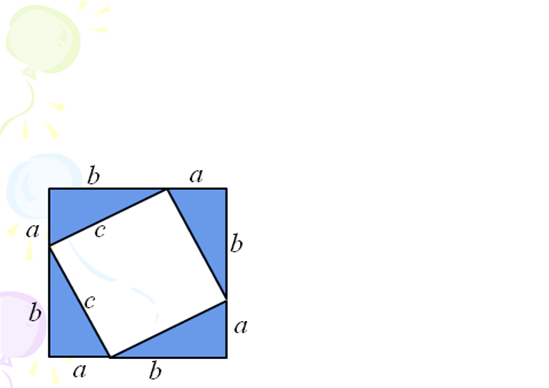
Дано: Прямоугольный треугольник Доказать:

Доказательство: 1)Достроим треугольник до квадрата со стороной a+b

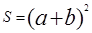
2) S большого квадрата квадрату его стороны, т.е

С другой стороны: S большого квадрата равна площади маленького квадрата плюс четыре площади треугольников (треугольники равны по двум катетам)

Докажем, что маленький четырёхугольник- квадрат:

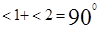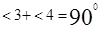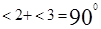
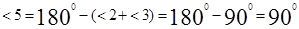Из равенства треугольников следует, что <1=<3, <2=<4, значит,

=, значит это квадрат

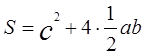Итак, S большого квадрата равна площади маленького квадрата плюс четыре площади треугольников, т.е

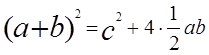3) Приравняем площади:

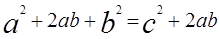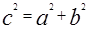
После упрощений получаем:

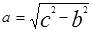
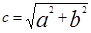Следствия:

Пифагоровы тройки:

5,4,3

13,12,5

17,5,8

10,8,6

Билет 11. Определение подобных треугольников. Отношение площадей и периметров

подобных треугольников (доказательство одного на выбор одной из теорем)

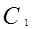
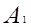
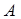
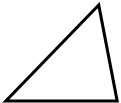Определение. Два треугольника называются подобными, если их углы соответственно равны, а сходственные стороны одного треугольника пропорциональны сходственным сторонам другого треугольника

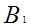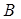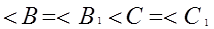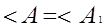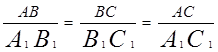Т.е 1)

2)

Теорема 1. Отношение периметров подобных треугольников равно коэффициенту подобия.

Теорема 2. Отношение площадей подобных треугольников равно квадрату коэффициенту подобия.

Я буду доказывать теорему 1

---

Дата добавления: 2015-08-17