Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.

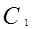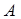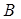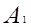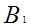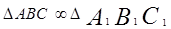
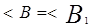
Дано:,

Доказать, что

Доказательство:

1)

, значит,

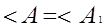Равенство всех углов доказано.

2) Т.к, то площади относятся как произведение сторон, заключающих эти углы, т.е (1)

Т.к, то аналогично (2)

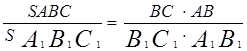
Т.к, то (3)

3) Приравням равенства (1) и (2) = и сократим на

, получим:

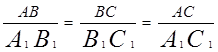Приравнивая равенства (2) и (3) получим:

Значит,. Получили, что углы равны и стороны

пропорциональны, т.е треугольник подобны (по определению)

(если спросят, сказать)

Определение. Два треугольника называются подобными, если их углы соответственно равны, а сходственные стороны одного треугольника пропорциональны сходственным сторонам другого треугольника

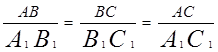
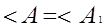Т.е 1)

2)

Билет 13. Средняя линия треугольника. Теорема о средней линии треугольника»

· Средней линией треугольника, называется отрезок соединяющий середины двух сторон треугольника.

Теорема:

·

N

М

С

В

А

Средняя линия треугольника параллельна одной из его сторон, а её длина равна половине этой стороны.

Доказательство:

1. Рассмотрим MBN и ABC

<B- общий

, значит

MBN∞ ABC (по 2 признаку подобия треугольников),

2. Т.к. MBN ∞ ABC, то

<1=<2, и они называются соответственные значит

MN||AC (по 2 признаку параллельных прямых)

, значит 2MN=AC, MN=

Билет 14. Понятие синуса, косинуса и тангенса острого угла прямоугольного

треугольника. Таблица основных углов с доказательством.

Соотношение между сторонами и углами прямоугольного треугольника.

Синусом острого угла прямоугольного треугольныка называется отношение противолежащего катета к гипотену

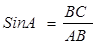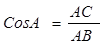Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе

---

Дата добавления: 2015-08-17