Тангенсом острова угла прямоугольного треугольника называется отношение синуса к косинусу этого угла

Таблица основных углов

SinA
CosA
TgA

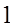
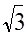
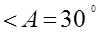
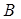Докажу первый столбик таблицы

Если, то, т.к катет,

лежащий против угла в равен половине гипотенузы.

Итак,.

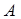
Найдём косинус по формуле:

Билет 15. Касательная к окружности. Свойство касательной. (Доказательство свойства касательной)

Определение: Прямая называется касательной к окружности если она имеет с окружностью одну общую точку.

Теорема.Свойства касательной: Касательная к окружности перпендикулярна к радиусу проведенной точки касания.

Дано: Окр (О,r=ОА), р- касательная, А- точка касания

Доказать, что

Доказательство:

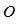
Доказательство:

Будем доказывать методом от противного. Предположим, что р не перпендикулярна ОА.В этом случае радиус ОА является наклонной к прямой р. Так как перпендикуляр, проведённый из точки О к прямой р, меньше наклонной ОА, то расстояние от центра О окружности до прямой р меньше радиуса. Следовательно, прямая р и окружность имеют две общие точки, т. е. р – секущая. Но это противоречит условию теоремы, что р - касательная к окружности. Так как получили противоречие, то предположение, что р не перпендикулярно ОА было неверным, значит, р перпендикулярна ОА.

Итак, касательная к окружности перпендикулярна к радиусу, проведённому в точку касания.

Билет 16. Свойство отрезков касательных.(доказательство теоремы)

Теорема(Свойство отрезков касательных). Отрезки касательных, проведенные из одной точки к окружности, равны и образуют равные углы с прямой, проходящей через эту точку и центр окружности.

Дано: АВ и АС – отрезки касательных

Доказать, что 1) АВ=АС 2) <1=<2

Доказательство:

Рассмотрим треугольник АВО и АСО. ОВ перпендикулярен АВ, а ОС – перпендикулярен АС(по свойству касательных). Прямоугольные треугольники АВО и АСО равны по катету и гипотенузе (ОВ=ОС – радиусы одной окружности, АО – общая гипотенуза). Поэтому равны и их катеты АВ=АС и углы ОАС и ОАВ, т.е <1=<2

Билет 17. Центральный угол. Вписанный угол. Теорема о вписанном угле(с доказательством)

---

Дата добавления: 2015-08-17