Каждой прямой , проходящей через две его соседние вершины.

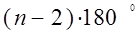Теорема. Сумма углов выпуклого n- угольника равна

Доказательство:

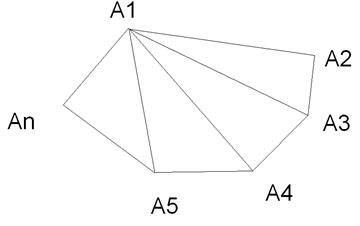
1) Проведем все диагонали из вершины А1.

2) Сумма углов многоугольника складывается из суммы углов всех треугольников, входящих в него,. Сумма углов одного треугольника равна 180 градусов,значит сумма углов многоугольника равна (n-2)180 градусов.

Билет 2. Параллелограмм. Свойства параллелограмма(доказательство одного на выбор)

Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны

Параллелограмм имеет два свойства.

Свойство 1. В параллелограмме противоположные стороны и углы равны.

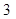
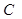
Дано: ABCD- пар-м

Д-ть: 1) AB=CD, ВС=АD

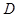
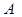2)<A=<C, <B=<D

Доказательство:

1) Проводим диагональ AC

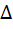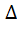2) Рассм. ABC и BDC

<1=<3(накрест.леж; по 1 св. пар. пр.)

<2=<4(аналогично),

BC- общая,

зн. 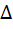ABC = 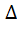BDC(по 2 приз. рав. тр.)

3) Из рав. тр. следует, что BC=AD, AB=CD,<B=<D, <A=<1+<2,<С=<4+<3,

зн. <A=<С

Следствие.

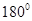Сумма углов параллелограмма, прилежащих к одной стороне, равна

Свойство 2. Диагонали параллелограмма пересекаются в одной точке и делятся в ней пополам.

Билет 3 Признаки параллелограмма (доказательство одного на выбор)

Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны

Существуют три признака параллелограмма

Признак 1 Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник параллелограмм.

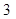
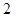
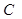
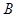Дано: ABCD- четырехугольник, AB= CD,

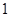
AB ll CD

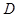
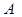Д-ть: ABCD- пар-м

Док-во:

1)Проведем диагональ AC

2) 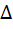ABC = ADC по 1 признаку равенства треугольников

(т.к. AB=CD- по усл., AC – общая, <1=<2(накрестлежащие))

3)Из рав. тр. следует, что <3=<4, зн. BC ll AD (по 1 признаку

параллельных прямых)

4) Итак, имеем: AB ll CD и BC ll AB, зн. ABCD- пар-м(по определению)

Признак 2 Если в четырехугольнике противополож. стороны попарно равны, то этот четырехугольник параллелограмм.

Признак 3 Если в четырехугольнике диагонали пересекаются, и точка пересечения делит их пополам, то этот четырехугольник параллелограмм.

Билет 4. Трапеция. Виды трапеций. Свойства равнобедренной трапеции

(доказательство одного на выбор)

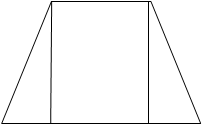Трапецией называется такой четырехугольник, у которого две стороны параллельны, а две другие не параллельны.

Виды трапеций

Обычная Прямоугольная

Равнобедренная

Трапеция называется равнобедренной, если ее боковые стороны равны.

Трапеция называется прямоугольной, если два ее угла прямые.

См.продолжение

---

Дата добавления: 2015-08-17