Читайте также:
|
Свойство 1. В равнобедренной трапеции углы при основании равны.
Дано: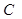 
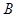
ABCD- равнобедренная трапеция.
Д-ть: <А= <D; <B= <C.
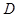
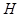
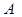
Д-во:
1. Проведем высоты BH и 
2. 
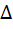ABH=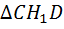 
(по катету и гиппотенузе), т. к. AB=CD(трапеция равнобедренная), BH=CH(т.к. 
- пар-м).
3. Из равенства тр. Следует, что <A=<D
4. <A+<B =180 
<C+ <D=180
<B =180 -<A,
<C=180 -<D,
зн. <B =<C
Свойство 2.В равнобедренной трапеции диагонали равны.
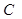
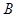
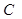Дано: ABCD- равнобедренная трапеция.
Д-ть: AC=BD
Д-во:
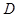
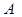1) Рассмотрим 
BDA и ACD
AD – общая,
<A=<D (по 1 св. равнобед. трап.),
BA=CD (т.к трапеция ранобедренная),
зн. BDA=ACD (по 1 приз. равенства тр)
2).Из рав. тр. следует, что AC=BD
Билет 5.Прямоугольник.Свойство диагоналей прямоугольника.
Прямоугольником называется параллелограмм, у которого все углы прямые.
Прямоугольник обладает всеми свойствами параллелограмма, но у него есть особое свойство. Докажем его.
 | |||||||||
 | |||||||||
 | |||||||||
| | ||||||||
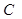
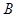
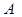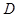Теорема. Диагонали прямоугольника равны.
Дано: АВСД-прямоугольник
Доказать: ВД=АС
Доказательство:
1)Рассмотрим: АВД и АСД- прямоугольные
АВ=СД(по 1 свойству параллелограмма)
АД -общая
Значит АВД= АСД (по 2-м катетам)
2)Из равенства треугольников следует, что АС=ВД
Билет 6. Ромб. Квадрат. Их свойства. Доказательство основного свойства ромба.
Дата добавления: 2015-08-17; просмотров: 396 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Каждой прямой , проходящей через две его соседние вершины. | | | Ромбом называется параллелограмм, все стороны которого равны. |