Геометрический смысл двойного интеграла.

Рассмотрим тело V, ограниченное частью поверхности, задаваемой уравнением z = f(x, y), проекцией D этой поверхности на плоскость Оху и боковой цилиндрической поверхностью, полученной из вертикальных образующих, соединяющих точки границы поверхности с их проекциями.

Будем искать объем этого тела как предел суммы объемов цилиндров, основаниями которых являются части ΔSi области D, а высотами – отрезки длиной f(Pi), где точки Pi принадлежат ΔSi. Переходя к пределу при 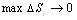, получим, что

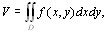(7.12)

то есть двойной интеграл представляет собой объем так называемого цилиндроида, ограниченного сверху поверхностью z = f(x, y), а снизу – областью D.

Теорема существования тройного интеграла. Если подынтегральная функция непрерывна на области V, то она интегрируема по этой области.

Вычисление тройного интеграла сводится к последовательному вычислению обыкновенных (однократных) интегралов.

Пусть функции f (x,y,z) и g (x,y,z) интегрируемы в области U. Тогда справедливы следующие свойства:

1. 

1. 

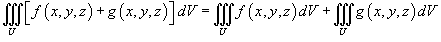
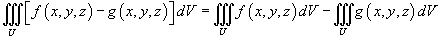
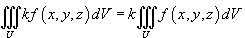1. , где k - константа;

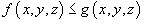1. Если в любой точке области U, то ;

1. Если область U является объединением двух непересекающихся областей U ₁ и U ₂, то ;

1. Пусть m - наименьшее и M - наибольшее значение непрерывной функции f (x,y,z) в области U. Тогда для тройного интеграла справедлива оценка:

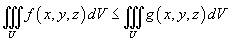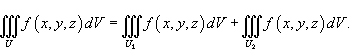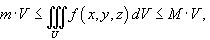
где V - объем области интегрирования U.

1. Теорема о среднем значении тройного интеграла.
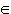   Если функция f (x,y,z) непрерывна в области U, то существует точка M ₀ U, такая, что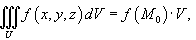

где V - объем области U.

26. Приложения тройного интеграла: объем тела, масса, координаты центра тяжести, геометрические моменты инерции.

Дата добавления: 2015-08-20