|
Читайте также: |
Предположим, что электрический заряд распределен по области R в плоскости O xy и его плотность распределения задана функцией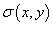 
. Тогда полный заряд пластины Q определяется выражением
25. Тройной интеграл: определение, геометрический смысл, теорема существования, свойства, вычисление, теорема о среднем значении.
Тройной интеграл от функции U=f(x,y,z), распространенным на область V, называется предел соответствующей трехкратной суммы.
Дата добавления: 2015-08-20; просмотров: 70 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Масса и статические моменты пластины | | | Геометрический смысл двойного интеграла. |