
Читайте также:
|
Площадь поверхности вращения, образующейся при вращении вокруг оси Ox дифференцируемой кривой, определяется по формулам (в зависимости от способа задания)
 (
( - длина окружности кольца,
- длина окружности кольца,  - его ширина).
- его ширина).
20. Физические приложения определенного интеграла: статические моменты и моменты инерции плоских дуг и фигур, нахождение координат центра тяжести, теоремы Гульдена, вычисление работы и давления
Путь S, пройденный телом при прямолинейном движении со скоростью v(t) за интервал времени от t 1 до t 2, вычисляется по формуле

Вычисление работы с помощью определённого интеграла.
Пусть под действием некоторой силы  материальная точка М движется по прямой в направлении оси OX. Требуется найти работу, произведённую силой
материальная точка М движется по прямой в направлении оси OX. Требуется найти работу, произведённую силой  при перемещении точки М из положения
при перемещении точки М из положения 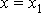 в положение
в положение  .
.
1) Если сила постоянна  , то работа выражается следующим образом
, то работа выражается следующим образом  .
.
2) Если сила переменная величина, то  .
.
Теоремы Гульдена Выведем теоремы, связывающие площадь поверхности (соответственно, объем тела) вращения с центром тяжести вращающейся дуги (соответственно, криволинейной трапеции).
Пусть поверхность  образована вращением дуги
образована вращением дуги 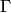 , имеющей длину
, имеющей длину  . Мы знаем, что ордината центра тяжести этой дуги выражается формулой
. Мы знаем, что ордината центра тяжести этой дуги выражается формулой

Так как площадь поверхности вращения выражается интегралом
 то из этого равенства следует, что
то из этого равенства следует, что  .
.
Мы доказали следующее утверждение, называемое первой теоремой Гульдина–Паппа.
Площадь поверхности, полученной от вращения кривой вокруг непересекающей ее оси, равна произведению длины  дуги этой кривой на длину окружности, описанной центром тяжести
дуги этой кривой на длину окружности, описанной центром тяжести 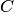 этой кривой.
этой кривой.
Аналогично, из формулы, выражающей ординату центра тяжести криволинейной трапеции
 и формулы объема тела вращения
и формулы объема тела вращения 
получаем  , т. е. следующее утверждение, называемое второй теоремой Гульдина–Паппа:
, т. е. следующее утверждение, называемое второй теоремой Гульдина–Паппа:
Объем тела, полученного от вращения плоской фигуры вокруг непересекающей ее оси, равен произведению площади этой фигуры на длину окружности, описанной центром тяжести этой фигуры.
Пользуясь этими двумя теоремами, можно в ряде случаев упростить процесс вычисления поверхности или объема тела вращения.
21. Несобственные интегралы: определение, признаки сравнения
Определённый интеграл называется несобственным, если выполняется, по крайней мере, одно из следующих условий.
· Область интегрирования является бесконечной. Например, является бесконечным интервалом  .
.
· Функция f(x) не ограничена в области интегрирования.
Пусть функции f(x) и g(x) интегрируемы по любому отрезку [a,b] и при  удовлетворяют неравенствам
удовлетворяют неравенствам  . Тогда:
. Тогда:

22. Двойной интеграл: определение, геометрический смысл, свойства, правила вычисления, замена переменных
Двойным интегралом называется предел двойной интегральной суммы при условии стремления к нулю диаметров всех ячеек, если он существует и не зависит он способа разбиения области D, от способа выбора ячеек Ci,j(xi,yj) внутри каждой ячейки 
Геометрический смысл: двойной интеграл от функции f(x,y)≥0 на области S равен объему цилиндрического тела с основанием S и ограниченного сверху поверхностью z=f(x,y)
Двойной интеграл обладает следующими свойствами:

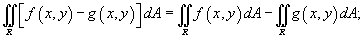
 , где k - константа;
, где k - константа;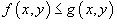 в области R, то
в области R, то 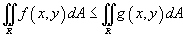 ;
; , то
, то  ;
; .
.  означает объединение этих двух областей.
означает объединение этих двух областей.Двойной интеграл вычисляется через повторные или двукратные интегралы. Различаются два основных вида областей интегрирования.
1) Область интегрирования S ограничена прямыми х=а, х=b и кривыми y=φ1(x), y=φ2(x),
Для такой области двойной интеграл вычисляется через повторный по формуле:

Сначала вычисляется внутренний интеграл:
При вычислении внутреннего интеграла ‘у’ считается переменной, а ‘х’-постоянной.
2) Область интегрирования S ограничена прямыми у=С, у=d и кривыми x=ψ1(y), x=ψ2(y)
Для такой области двойной интеграл вычисляется через повторный по формуле:

Сначала вычисляется внутренний интеграл, затем внешний.
При вычислении внутреннего интеграла ‘х’ считается переменной, а ‘у’-постоянной.
3) Если область интегрирования не относится ни к 1 ни ко второму случаю, то разбиваем ее на части таким образом, чтобы каждая из частей относилась к одному из этих двух видов.
Замена переменных в двойном интеграле описывается формулой
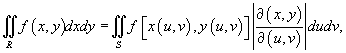
Итак, замена переменных в двойном интеграле производится с помощью следующих трех шагов:
 ;
;23. Геометрические приложения двойного интеграла: площадь плоской фигуры, объем тела, площадь поверхности
Дата добавления: 2015-08-20; просмотров: 108 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Интегральная сумма, определенный интеграл (определение, теорема существования, основные свойства, правила вычисления) | | | Площадь плоской фигуры |