Скалярное поле, производная по направлению, градиент, их свойства.

Скалярным полем называется часть пространства (или все пространство), каждой точке M которой соответствует численное значение некоторой скалярной величины u. Скалярная величина u не зависит от времени, а зависит только от положения точки M в пространстве, это значит, рассматривается как функция точки M: u = f(M). Эта функция называется функцией поля. Если в пространстве выбрана система координат Oxyz, то скалярная величина u является функцией координат x, y, z, т.е. u = f(M)= f(x, y,z)

Наоборот, каждая функция трех переменных u = f(x, y,z) задает некоторое скалярное поле.

Геометрическим изображением скалярного поля являются поверхности уровня.

Пусть в некоторой области D задана функция u=u(x,y,z) и точка M(x,y,z). Проведем из точки M вектор , направляющие косинусы которого cos α, cos β, cos γ. На векторе , на расстоянии от его начала рассмотрим точку , т.е. .

.
Пусть в каждой точке некоторой области D задана функция u=u(x,y,z).
Вектор, проекциями которого на оси координат являются значения частных производных этой функции в соответствующей точке, называется градиентом функции u=u(x,y,z) и обозначается grad u или ⍢ u: .

При этом говорят, что в области D определено векторное поле градиентов.

Для нахождения градиента функции u=u(x,y,z) в заданной точке M₀(x₀,y₀,z₀) используют формулу:
.

10. Первообразная. Неопределенный интеграл: его свойства, геометрический смысл.

Первообразной функции f(x) на промежутке (a; b) называется такая функция F(x), что выполняется равенство F’(x)=f(x) для любого х из заданного промежутка.

Если принять во внимание тот факт, что производная от константы С равна нулю, то справедливо равенство (F(x)+C)’=f(x). Таким образом, функция f(x) имеет множество первообразных F(x)+C, для произвольной константы С, причем эти первообразные отличаются друг от друга на произвольную постоянную величину.

Все множество первообразных функции f(x) называется неопределенным интегралом этой функции и обозначается .

Выражение f(x)dx называют подынтегральным выражением, а f(x) – подынтегральной функцией. Подынтегральное выражение представляет собой дифференциал функции f(x).

Действие нахождения неизвестной функции по заданному ее дифференциалу называется неопределенным интегрированием, потому что результатом интегрирования является не одна функция F(x), а множество ее первообразных F(x)+C.

На основании свойств производной можно сформулировать и доказать свойства неопределенного интеграла (свойства первообразной).

1.
Производная результата интегрирования равна подынтегральной функции.

2.
Неопределенный интеграл дифференциала функции равен сумме самой функции и произвольной константы.

3. , где k – произвольная константа.
Коэффициент можно выносить за знак неопределенного интеграла.

4.
Неопределенный интеграл суммы/разности функций равен сумме/разности неопределенных интегралов функций.

Промежуточные равенства первого и второго свойств неопределенного интеграла приведены для пояснения.

Для доказательства третьего и четвертого свойств достаточно найти производные от правых частей равенств:

Эти производные равны подынтегральным функциям, что и является доказательством в силу первого свойства. Оно же используется в последних переходах.

Геометрически неопределенный интеграл представляет собой семейство «параллельных» кривых линий y=F(x)+C. График каждой первообразной называется интегральной кривой.

Таблица основных интегралов.

12. Основные методы интегрирования: подведение функции под знак дифференциала, интегрирование методом разложения, интегрирование методом замены переменной (непосредственное, подстановкой), интегрирование по частям.

Метод подведения под знак дифференциала основан на равенстве .

То есть, главной задачей является приведение подынтегральной функции к виду f(g(x))d(g(x)).

Пусть требуется найти неопределенный интеграл ∫f(x)dx. Предположим, что существуют дифференцируемые функци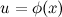и и такие, что

Тогда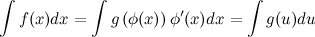

Указанное преобразование подынтегрального выражения называют подведением под знак дифференциала.

Тогда, если ∫f(x)dx=F(x)+c и 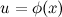, то имеет место следующее равенство: ∫f(u)du=F(u)+C

Рассмотрим функции u=u(x) и v=v(x), которые имеют непрерывные производные. Согласно свойствам дифференциалов, имеет место следующее равенство: d(uv)=udv+vdu

Проинтегрировав левую и правую части последнего равенства, получим:

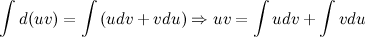
Полученное равенство перепишем в виде: ∫udv=uv-∫vdu

Эта формула называется формулой интегрирования по частям. С ее помощью интеграл ∫udv можно свести к нахождению интеграла ∫vdu, который может быть более простым.

Замена переменной.

Пусть требуется найти неопределенный интеграл 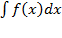. Сделаем замену в подынтегральном выражении, положив x=φ(t), где φ(t) — монотонная непрерывная функция, которая имеет непрерывную производную. Тогда dx= φ’(t)dt. В этом случае имеет следующее равенство:

Дата добавления: 2015-08-20