
Читайте также:
|
Полным приращением функции называется такое приращение, при котором одновременно изменяются все ее переменные.
∆z=f(x+∆x,y+∆y)-f(x,y)
Пусть функция z=f(x,y) непрерывна и имеет непрерывные частные производные fx’(x,y) и fy’(x,y). Зафиксируем пару значений x и y и дадим им приращения ∆x и ∆y.
Тогда функция получит приращение, ∆z=f(x+∆x,y+∆y)-f(x,y), которое называется полным приращением. Запишем ∆z следующим образом: ∆z=(f(x+∆x,y+∆y)-f(x,y+∆y))+(f(x,y+∆y)-f(x,y)) (3).
Каждое из выражений в скобках представляет собой частное приращение функции z. Применим к этим выражениям формулу Лагранжа:
 ,
,

Где  а
а  . Если
. Если 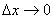 и
и  то
то  . Значит, в силу непрерывности частных производных, при
. Значит, в силу непрерывности частных производных, при 
 . Таким образом,
. Таким образом, 
 , где
, где  и
и 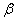 бесконечно малые величины. Отсюда:
бесконечно малые величины. Отсюда: 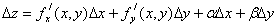 (4).
(4).
Обозначим  Тогда
Тогда  , где
, где  . Так как
. Так как  ,
,  , поэтому
, поэтому  . Значит, при
. Значит, при 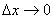 и
и  ,
,  также стремиться к нулю. Соотношения
также стремиться к нулю. Соотношения  равносильны соотношению
равносильны соотношению  . Окончательно,
. Окончательно,
 (5)
(5)
причем  . Формула (5) называется формулой полного приращения функции. Сумма первых двух слагаемых есть выражение линейное относительно ∆x и ∆y и представляет собой главную часть приращения, отличаясь от ∆z на бесконечно малую высшего порядка относительно ∆p. Линейная часть приращения называется полным дифференциалом функции и обозначается dz.
. Формула (5) называется формулой полного приращения функции. Сумма первых двух слагаемых есть выражение линейное относительно ∆x и ∆y и представляет собой главную часть приращения, отличаясь от ∆z на бесконечно малую высшего порядка относительно ∆p. Линейная часть приращения называется полным дифференциалом функции и обозначается dz. 
 .
.
Приращения независимых переменных ∆x и ∆y равны дифференциалам независимых переменных, т.е. dx=∆x и dy=∆y. Тогда 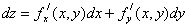 . Равенство (5) можно переписать в виде:
. Равенство (5) можно переписать в виде:  ,и, с точностью до бесконечно малой высшего порядка относительно ∆p можно записать приближенное равенство:
,и, с точностью до бесконечно малой высшего порядка относительно ∆p можно записать приближенное равенство:  , причем точность этого равенства тем выше, чем меньше приращения аргументов.
, причем точность этого равенства тем выше, чем меньше приращения аргументов.
Дата добавления: 2015-08-20; просмотров: 147 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Экстремум функции двух переменных, условный экстремум, наибольшее и наименьшее значение функции в замкнутой области. | | | Дифференциалы высших порядков от функции двух аргументов. |