Дифференциалы высших порядков от функции двух аргументов.

Пусть у=ƒ(х) дифференцируемая функция, а ее аргумент х — независимая переменная. Тогда ее первый дифференциал dy=ƒ'(х)dx есть также функция х; можно найти дифференциал этой функции.

Дифференциал от дифференциала функции у=ƒ(х) называется ее вторым дифференциалом (или дифференциалом второго порядка) и обозначается d²y или d²ƒ(х).

Итак, по определению d²y=d(dy). Найдем выражение второго дифференциала функции у=ƒ(х).

Так как dx=∆х не зависит от х, то при дифференцировании считаем dx постоянным:

d²y=d(dy)=d(f'(x)dx)=(ƒ'(х)dx)'•dx=f"(x)dx•dx=f"(x)(dx)² т. е.

d²y=ƒ"(х)dх². (24.5)

Здесь dx² обозначает (dx)².

Аналогично определяется и находится дифференциал третьего порядка

d³y=d(d²y)=d(ƒ"(х)dx²)≈f'(x)(dx)³.

И, вообще, дифференциал n-го порядка есть дифференциал от дифференциала (n-1)-го порядка: dⁿy=d(d^n-ly)=f⁽ⁿ⁾(x)(dx)ⁿ.

Отсюда находим, что 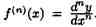, В частности, при n=1,2,3

соответственно получаем:

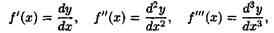
т. е. производную функции можно рассматривать как отношение ее дифференциала соответствующего порядка к соответствующей степени дифференциала независимой переменной.

Отметим, что все приведенные выше формулы справедливы только, если х — независимая переменная. Если же функцию у=ƒ(х), где х — функция от кαкой-тo другой независимой переменной, то дифференциалы второго и выше порядков не обладают свойством инвариантности формы и вычисляются по другим формулам. Покажем это на примере дифференциала второго порядка.

Используя формулу дифференциала произведения (d(uv)=vdu+udv), получаем:

d²y=d(f'(x)dx)=d(ƒ'(х))dx+ƒ'(х)•d(dx)=ƒ"(х)dx•dx+ƒ'(х)•d²x, т. е.

d²y=ƒ"(х)dx²+ƒ'(х)•d²x. (24.6)

Сравнивая формулы (24.5) и (24.6), убеждаемся, что в случае сложной функции формула дифференциала второго порядка изменяется: появляется второе слагаемое ƒ'(х)•d²х.

Ясно, что если х — независимая переменная, то

d²x=d(dx)=d(l•dx)=dx•d(l)=dx•0=0

и формула (24.6) переходит в формулу (24.5).

Дата добавления: 2015-08-20