Частные приращения функции двух аргументов, частные производные первого порядка, частные производные высших порядков

Частным приращением функции называется такое ее приращение, при котором изменяется только одна из всех переменных.

Приращение по х (2), приращение по у(3)

Частные производные первого порядка. Если существует конечный предел отношения частного приращения по x функции f(x,y) в точке M₀(x₀,y₀) к вызвавшему его приращению Δx при Δx ⇾0, то этот предел называется частной производной по х функции z=f(x,y) в точке М₀

Частные производные высших порядков. Частные производные функции нескольких переменных являются функциями тех же переменных. Эти функции, в свою очередь, могут иметь частные производные, которые называются частными производными второго порядка исходной функции.

Так, например, функция z = f(x, y) двух переменных имеет четыре частные производные второго порядка

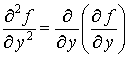
Частные производные от частных производных второго порядка называются частными производными третьего порядка. Функция имеет восемь частных производных третьего порядка. Частная производная второго или более высокого порядка, взятая по нескольким разным переменным, называется смешанной частной производной.

Дата добавления: 2015-08-20