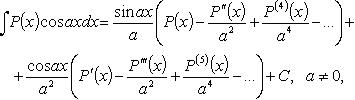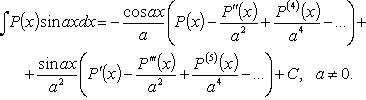Интегрирование некоторых трансцендентных функций.
Геометрический смысл функции 2-х переменных | Частные приращения функции двух аргументов, частные производные первого порядка, частные производные высших порядков | Сложные функции и их дифференцирование. | Неявные функции и их дифференцирование. | Экстремум функции двух переменных, условный экстремум, наибольшее и наименьшее значение функции в замкнутой области. | Полное приращение и полный дифференциал функции двух аргументов первого порядка. Применение полного дифференциала к приближенным вычислениям. | Дифференциалы высших порядков от функции двух аргументов. | Касательная плоскость и нормаль к поверхности в заданной точке. | Скалярное поле, производная по направлению, градиент, их свойства. | Интегрирование тригонометрических функций |
1.  - многочлен.
- многочлен.
Интеграл можно вычислять интегрированием по частям или методом неопределенных коэффициентов, отыскивая результат в виде
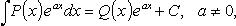
где Q(x) - многочлен той же степени, что и P(x).
Имеет место результат
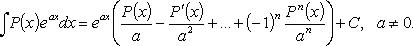
2.  - многочлен.
- многочлен.
Кроме интегрирования по частям, можно пользоваться формулами:
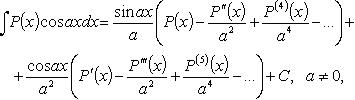
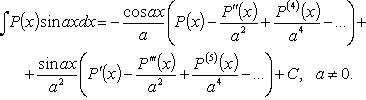
Дата добавления: 2015-08-20; просмотров: 129 | Нарушение авторских прав
mybiblioteka.su - 2015-2025 год. (0.004 сек.)

 - многочлен.
- многочлен.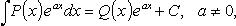
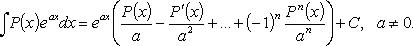
 - многочлен.
- многочлен.